题目内容
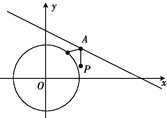
【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”,即将军在观望烽火之后从山脚下某处出发,先到河边饮马再回到军营,怎样走才能使总路程最短?在如图所示的直角坐标系xOy中,设军营所在平面区域为{(x,y)|x2+y2≤![]() },河岸线所在直线方程为x+2y-4=0.假定将军从点P(
},河岸线所在直线方程为x+2y-4=0.假定将军从点P(![]() ,
,![]() )处出发,只要到达军营所在区域即回到军营,当将军选择最短路程时,饮马点A的纵坐标为______.最短总路程为______
)处出发,只要到达军营所在区域即回到军营,当将军选择最短路程时,饮马点A的纵坐标为______.最短总路程为______
【答案】![]()
![]()
【解析】
求出P(![]() ,
,![]() )关于直线x+2y
)关于直线x+2y![]() 4=0的对称点P'的坐标,再求出线段OP'与直线x+2y-4=0的交点A,再利用圆的几何性质可得结果.
4=0的对称点P'的坐标,再求出线段OP'与直线x+2y-4=0的交点A,再利用圆的几何性质可得结果.
设P(![]() ,
,![]() )关于直线x+2y
)关于直线x+2y![]() 4=0的对称点为P'(m,n),
4=0的对称点为P'(m,n),
则 解得
解得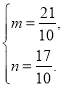
因为从点P到军营总路程最短,所以A为线段OP'与直线x+2y![]() 4=0的交点,
4=0的交点,
联立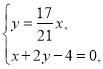 得y=
得y=![]() (4
(4![]() 2y),解得y=
2y),解得y=![]() .
.
所以“将军饮马”的最短总路程为![]()
![]()
![]() =
=![]() ,故答案为
,故答案为![]() ,
,![]() .
.

【题目】网上购物是用户使用手机或电脑对所消费的商品或服务进行网络账务支付的一种服务方式,外卖、购物、买票等等我们生活的各个方面都可以通过网上来实现,某网络公司通过随机问卷调查,得到不同年龄段的网民在网上购物的情况.并从参与调查者中随机抽取了![]() 人.经统计得到如下表格:
人.经统计得到如下表格:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
在网上购物的人数 |
|
|
|
|
|
|
若把年龄大于或等于![]() 而小于
而小于![]() 岁的视为青少年,把年龄大于或等于
岁的视为青少年,把年龄大于或等于![]() 而小于
而小于![]() 岁的视为中年.把年龄大于或等于
岁的视为中年.把年龄大于或等于![]() 岁的视为老年,将频率视为概率.求:
岁的视为老年,将频率视为概率.求:
(1)在青少年,中年,老年中,哪个群休网上购物的概率最大?
(2)现从某市青少年网民(人数众多)中随机抽取![]() 人,设其中网上购物的人数为
人,设其中网上购物的人数为![]() .求随机变量
.求随机变量![]() 的分布列及期望.
的分布列及期望.
【题目】2019年初,某高级中学教务处为了解该高级中学学生的作文水平,从该高级中学学生某次考试成绩中按文科、理科用分层抽样方法抽取![]() 人的成绩作为样本,得到成绩频率分布直方图如图所示,
人的成绩作为样本,得到成绩频率分布直方图如图所示,![]() ,参考的文科生与理科生人数之比为
,参考的文科生与理科生人数之比为![]() ,成绩(单位:分)分布在
,成绩(单位:分)分布在![]() 的范围内且将成绩(单位:分)分为
的范围内且将成绩(单位:分)分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六个部分,规定成绩分数在
六个部分,规定成绩分数在![]() 分以及
分以及![]() 分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.
分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.

(1)求实数![]() 的值;
的值;
(2)(i)完成下面![]() 列联表;
列联表;
文科生/人 | 理科生/人 | 合计 | |
优秀作文 | 6 | ______ | ______ |
非优秀作文 | ______ | ______ | ______ |
合计 | ______ | ______ | 400 |
(ii)以样本数据研究学生的作文水平,能否在犯错误的概率不超过![]() 的情况下认为获得“优秀作文”与学生的“文理科“有关?
的情况下认为获得“优秀作文”与学生的“文理科“有关?
注: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】随着生活节奏的加快以及停车日益困难,网约车越来越受到大众的欢迎.某网约车公司为了了解客户对公司的满意度,通过网络问卷的方式,随机调查了2000个客户,并通过随机抽样得到100个样本数据,统计后,得到如下频率分布表:
分组 |
|
|
|
|
|
|
|
频数 | 6 | 12 | 19 | 25 | 20 | 13 | 5 |
(1)根据频率分布表,可以认为满意度![]() ,其中
,其中![]() 近似看作是这100个样本数据的平均值,利用正态分布,求
近似看作是这100个样本数据的平均值,利用正态分布,求![]() ;
;
(2)该公司为参加网络问卷调查的客户提供了抽奖活动,活动规则:①若满意度不低于![]() ,可抽奖2次;若满意度低于
,可抽奖2次;若满意度低于![]() ,可抽奖1次;②每次抽奖可获得的优惠券金额为10元或20元,相应的概率均为
,可抽奖1次;②每次抽奖可获得的优惠券金额为10元或20元,相应的概率均为![]() .求参与网络问卷调查的客户人均可获得优惠券金额(单位:元).
.求参与网络问卷调查的客户人均可获得优惠券金额(单位:元).
(附:参考数据与公式:若![]() ,则
,则![]() ,
,![]() ,
,![]() .)
.)