题目内容
已知函数f(x)=sin (2x+φ),其中φ为实数,若f(x)≤ 对x∈R恒成立,且
对x∈R恒成立,且 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).
 对x∈R恒成立,且
对x∈R恒成立,且 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).A. =-1 =-1 |
B.f >f >f |
| C.f(x)是奇函数 |
D.f(x)的单调递增区间是 (k∈Z) (k∈Z) |
D
由f(x)≤ 恒成立知x=
恒成立知x=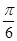 是函数的对称轴,即2×
是函数的对称轴,即2×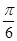 +φ=
+φ=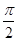 +kπ,k∈Z,所以φ=
+kπ,k∈Z,所以φ=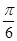 +kπ,k∈Z,又f
+kπ,k∈Z,又f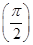 <f(π),所以sin (π+φ)<sin (2π+φ),即-sin φ<sin φ.所以sin φ>0,得φ=
<f(π),所以sin (π+φ)<sin (2π+φ),即-sin φ<sin φ.所以sin φ>0,得φ=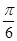 ,即f(x)=sin
,即f(x)=sin 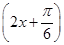 ,由-
,由-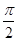 +2kπ≤2x+
+2kπ≤2x+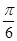 ≤
≤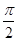 +2kπ,k∈Z,得-
+2kπ,k∈Z,得-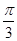 +kπ≤x≤
+kπ≤x≤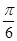 +kπ,k∈Z,即函数的单调递增区间是
+kπ,k∈Z,即函数的单调递增区间是 (k∈Z).
(k∈Z).
 恒成立知x=
恒成立知x=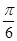 是函数的对称轴,即2×
是函数的对称轴,即2×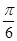 +φ=
+φ=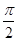 +kπ,k∈Z,所以φ=
+kπ,k∈Z,所以φ=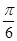 +kπ,k∈Z,又f
+kπ,k∈Z,又f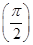 <f(π),所以sin (π+φ)<sin (2π+φ),即-sin φ<sin φ.所以sin φ>0,得φ=
<f(π),所以sin (π+φ)<sin (2π+φ),即-sin φ<sin φ.所以sin φ>0,得φ=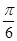 ,即f(x)=sin
,即f(x)=sin 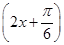 ,由-
,由-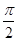 +2kπ≤2x+
+2kπ≤2x+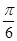 ≤
≤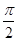 +2kπ,k∈Z,得-
+2kπ,k∈Z,得-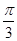 +kπ≤x≤
+kπ≤x≤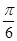 +kπ,k∈Z,即函数的单调递增区间是
+kπ,k∈Z,即函数的单调递增区间是 (k∈Z).
(k∈Z).
练习册系列答案
相关题目
 个单位,得到函数y=f(x)·sin x的图象,则f(x)的表达式可以是( ).
个单位,得到函数y=f(x)·sin x的图象,则f(x)的表达式可以是( ). sin 2x
sin 2x 中,
中, 分别为角
分别为角 的对边,
的对边,
 ,设角B的大小为x,用x表示c,并求c的取值范围.
,设角B的大小为x,用x表示c,并求c的取值范围. )的部分图像,其中A,B两点之间的距离为5,那么f(-1)=________.
)的部分图像,其中A,B两点之间的距离为5,那么f(-1)=________.
 =________.
=________. +
+ ,对任意实数
,对任意实数 都有
都有 且
且 ,则实数
,则实数
 ∪
∪
 ∪
∪

 的图象,只需把函数y=sin
的图象,只需把函数y=sin  的图象( ).
的图象( ). 个单位长度
个单位长度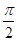 个单位长度
个单位长度
