题目内容
【题目】设函数![]() ,函数
,函数![]()
![]()
(1)当![]() 时,解关于
时,解关于![]() 的不等式:
的不等式: ![]() ;
;
(2)若![]() 且
且![]() ,已知函数
,已知函数![]() 有两个零点
有两个零点![]() 和
和![]() ,若点
,若点![]() ,
, ![]() ,其中
,其中![]() 是坐标原点,证明:
是坐标原点,证明: ![]() 与
与![]() 不可能垂直.
不可能垂直.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:代入b=1列出所要解的不等式,分解因式化为(ax-2)(x-1)<0,由于所等式含参,所以针对参数a进行分类讨论,求出解集;s和t为函数的零点就是二次方程的两个根,根据根与系数的关系,写出s,t与系数a,b的关系,假设OA与OB垂直,利用数量积为0,得出g(s)g(t)=-1,把根与系数关系中的s+t及st代入,利用基本不等式会产生矛盾,说明![]() 与
与![]() 不可能垂直.
不可能垂直.
试题解析:
(1)当![]() 时,由
时,由![]() 有
有![]() ,即
,即![]() ,当
,当![]() 时,有
时,有![]() ,解得:
,解得: ![]() 当
当![]() 时,
时, ![]() ,解得:
,解得: ![]() 或
或![]() ,当
,当![]() 时,
时, ![]() ,所以 当
,所以 当![]() 时,
时, ![]() ,解得:
,解得: ![]() 当
当![]() 时,
时, ![]() ,此时无解 当
,此时无解 当![]() 时,
时, ![]() ,解得:
,解得: ![]() ,综上: 当
,综上: 当![]() 时,原不等式的解集为:
时,原不等式的解集为:![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() .
.
(2)![]() 时, 由
时, 由![]() 为
为![]() 的两根可得,
的两根可得, ![]() ,
, ![]()
假设![]() ,即
,即![]() ,故
,故![]() ,即
,即![]() ,所以
,所以![]() 从而有
从而有![]() ,即
,即 ![]()
故![]() 即
即![]() ,这与
,这与![]() 矛盾.故
矛盾.故![]() 与
与![]() 不可能垂直.
不可能垂直.

 阅读快车系列答案
阅读快车系列答案【题目】某市为了普及法律知识,增强市民的法制观念,针对本市特定人群举办网上学法普法考试.为了解参考人群的法律知识水平,从一次普法考试中随机抽取了50份答卷进行分析,得到这50份答卷成绩的统计数据如下:
成绩分组 |
|
|
|
|
|
|
频数 | 2 | 5 | 12 | 16 | 10 | 5 |
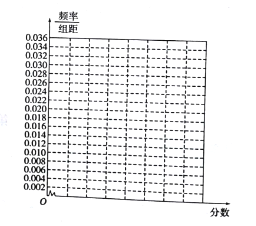
(1)在答题卡的图中作出样本数据的频率分布直方图;
(2)试根据统计数据,估计本次普法考试的平均成绩![]() 和中位数( 同一组中的数据用该组区间的中点值作代表);
和中位数( 同一组中的数据用该组区间的中点值作代表);
(3)已知该市有100 万人参加考试,得分低于60 分的需要重考(不低于60 分为合格,不再重考).若每次重考的合格率都比上一次考试低6 个百分点,试估计第3 次重考的人数.
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 工人数(人) |
19 | 1 |
28 | 3 |
29 | 3 |
30 | 5 |
31 | 4 |
32 | 3 |
40 | 1 |
合计 | 20 |
(1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.
【题目】稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+)+9500 (>0),已知第一、二季度平均单价如下表所示:
x | 1 | 2 | 3 |
y | 10000 | 9500 | ? |
则此楼群在第三季度的平均单价大约是 ( )
A.10000元
B.9500元
C.9000元
D.8500元