题目内容
(本题满分14分)已知函数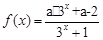 .
. 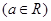
(1)是否存在实数 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;
(2)用单调性定义证明:不论 取任何实数,函数f(x)在其定义域上都是增函数;
取任何实数,函数f(x)在其定义域上都是增函数;
(3)若函数f(x)为奇函数,解不等式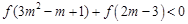 .
.
(1)当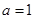 时,函数f(x)为奇函数;(2)证明:见解析。
时,函数f(x)为奇函数;(2)证明:见解析。
(3)
解析试题分析:(1)根据f(x)为奇函数,可确定f(-x)+f(x)=0恒成立.从而可得a值.
(2)利用单调性的定义证明分三个步骤:一取值,二作差变形判断差值符号,三确定单调性.
(3)利用单调性与奇偶性把不等式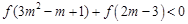 转化为
转化为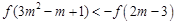 进一步转化为
进一步转化为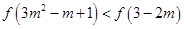 ,
,
然后利用单调性转化为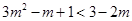 求解.
求解.
(1)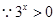
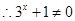 函数f(x)的定义域为
函数f(x)的定义域为 即
即 …1分
…1分
假设存在实数 使函数f(x)为奇函数,
使函数f(x)为奇函数,
由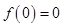 得
得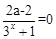 解得
解得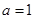 …2分,
…2分,

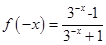
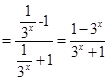
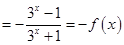
 当
当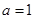 时,函数f(x)为奇函数……………4分
时,函数f(x)为奇函数……………4分
(2)证明:任取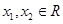 ,且
,且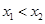
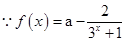
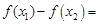
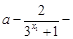
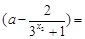
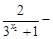
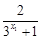
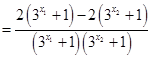
 …7分
…7分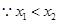 ,
,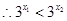
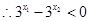
又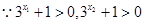
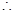
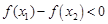 即
即
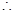 不论
不论 取何值,函数f(x)在其定义域上都是增函数. …………9分
取何值,函数f(x)在其定义域上都是增函数. …………9分
(3)由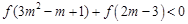 得
得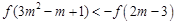
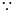 函数f(x)为奇函数
函数f(x)为奇函数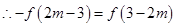

由(2)已证得函数 在R上是增函数
在R上是增函数
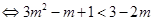
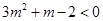
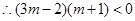
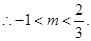
不等式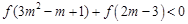 的解集为
的解集为 …………14分
…………14分
考点:函数的奇偶性,单调性的证明,解抽象函数的不等式,一元二次不等式.
点评:判定函数的奇偶性先确定定义域是否关于原点对称;利用单调性证明证明时要注意三个步骤一取值,作差变形,得出结论.变形的目的是判断差值符号.解抽象不等式要注意利用单调性脱掉法则符号f转化为普通不等式求解.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
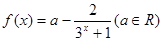 :
:  是
是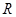 上的增函数;
上的增函数;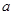 使函数
使函数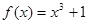 为R上的单调递增函数
为R上的单调递增函数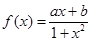 是定义在
是定义在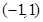 上的奇函数,且
上的奇函数,且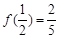 。
。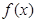 的解析式;
的解析式;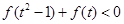 。
。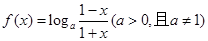
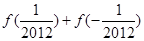 的值;
的值;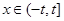 (其中
(其中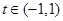 ,且
,且 为常数)时,
为常数)时,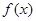 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如 时,求满足不等式
时,求满足不等式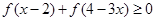 的
的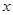 的范围.
的范围. 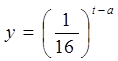 (a为常数),
(a为常数),
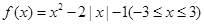
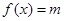 有两个根,试求
有两个根,试求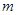 的取值范围。
的取值范围。 :
: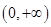 为单调递减函数;
为单调递减函数;  的奇偶性.
的奇偶性. 是偶函数.
是偶函数. 的值;
的值; ,其中
,其中 若函数
若函数 与
与 的图象有且只有一个交点,求
的图象有且只有一个交点,求 的取值范围.
的取值范围.