题目内容
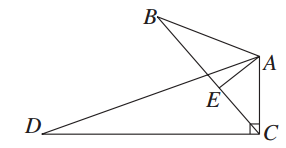
如图,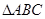 是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE,
是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE,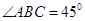 ,PD=1,DB=8.
,PD=1,DB=8.
(1)求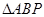 的面积;
的面积;
(2)求弦AC的长.
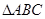 是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE,
是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE,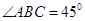 ,PD=1,DB=8.
,PD=1,DB=8.
(1)求
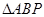 的面积;
的面积;(2)求弦AC的长.
(1)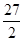 ;(2)
;(2)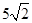 .
.
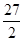 ;(2)
;(2)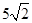 .
.试题分析:本题主要考查圆的切线的性质、切割线定理、勾股定理、三角形面积公式、相交弦定理等基础知识,考查学生的分析问题解决问题的能力、逻辑推理能力、计算能力.第一问,先利用切线的性质得到
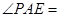
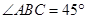 ,所以
,所以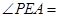
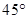 ,
,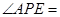
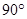 ,所以由切割线定理有
,所以由切割线定理有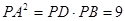 ,所以利用三角形面积求△
,所以利用三角形面积求△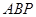 的面积为
的面积为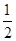
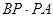
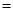
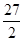 ;第二问,在
;第二问,在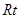 △
△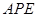 中,利用勾股定理得
中,利用勾股定理得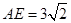 ,
,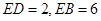 ,再由相交弦定理得出
,再由相交弦定理得出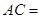
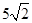 .
.(1)因为
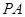 是⊙
是⊙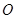 的切线,切点为
的切线,切点为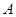 ,
,所以
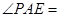
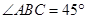 , 1分
, 1分又
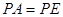 ,所以
,所以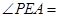
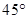 ,
,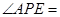
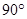 2分
2分因为
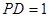 ,
,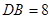 ,所以由切割线定理有
,所以由切割线定理有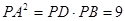 ,所以
,所以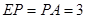 , 4分
, 4分所以△
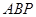 的面积为
的面积为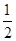
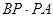
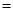
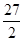 . 5分
. 5分(2)在
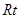 △
△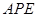 中,由勾股定理得
中,由勾股定理得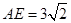 6分
6分又
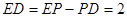 ,
, 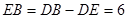 ,
,所以由相交弦定理得
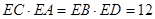 9分
9分所以
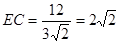 ,故
,故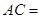
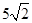 . 10分
. 10分
练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 ,BD是圆
,BD是圆 于点E,DA平分
于点E,DA平分 .
.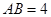 ,
,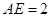 ,求CD.
,求CD.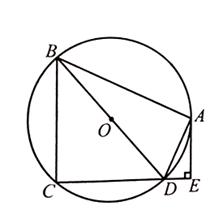
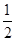 CD.
CD.
 是⊙
是⊙ 的直径
的直径 延长线上一点,
延长线上一点, 与⊙
与⊙ ,
, 的角平分线交
的角平分线交 于点
于点 ,则
,则 的大小为_________.
的大小为_________.
 PD.若PC=4,PB=2,则CD=____________.
PD.若PC=4,PB=2,则CD=____________.

 为圆
为圆 的直径,
的直径, ,过圆
,过圆 作圆
作圆 ,过点
,过点 于点
于点 ,若
,若 中点,则
中点,则 =_____.
=_____.