题目内容
(本小题满分13分)下列是真命题还是假命题，用分析法证明你的结论．
命题：若a>b>c且a＋b＋c＝0，则
.
命题：若a>b>c且a＋b＋c＝0，则
.真命题
此命题是真命题∵a＋b＋c＝0，a>b>c，∴a>0，c<0.
要证成立，只要证
.
即证b2－ac<3a2，也就是证：(a＋c)2－ac<3a2.即证(a－c)(2a＋c)>0.
∵a－c>0,2a＋c＝(a＋c)＋a＝a－b>0，
∴(a－c)(2a＋c)>0成立．故原不等式成立
要证
成立，只要证.即证b2－ac<3a2，也就是证：(a＋c)2－ac<3a2.即证(a－c)(2a＋c)>0.
∵a－c>0,2a＋c＝(a＋c)＋a＝a－b>0，
∴(a－c)(2a＋c)>0成立．故原不等式成立
练习册系列答案
阅读快车系列答案
相关题目
－
≥a＋
－2.
_______
．
>
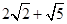”时，假设的内容应为______________．
中恰有一个偶数”正确的反设为（ ）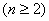
第2个数是________________.