Question

【题目】已知定义在R上的函数f（x）＝|x﹣m|+|x|，m∈N*，存在实数x使f（x）＜2成立．

（1）求不等式f（x）＞8的解；

（2）若α，β≥1，f（α）+f（β）＝4，求证：．

Answer 1

【答案】(1) {x|x或x}；(2)证明见解析

【解析】

（1）由绝对值三角不等式可得|x﹣m|+|x|≥|m|，根据存在实数x使f（x）＜2成立，求出实数m的值，然后解不等式f（x）＞8即可．

（2）先由条件求出α+β＝3，从而得到，再利用基本不等式求出最小值即可证明结论．

（1）因为|x﹣m|+|x|≥|（x﹣m）﹣x|＝|m|，

所以由存在实数x使f（x）＜2成立，可得|m|＜2，

所以﹣2＜m＜2，因为m∈N*，所以m＝1，

所以f（x）＝|x﹣1|+|x|．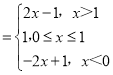

因为f（x）＞8，所以或，

所以x或x，

所以不等式的解集为{x|x或x}；

（2）因为α，β≥1，所以f（α）+f（β）＝2α﹣1+2β﹣1＝4，则α+β＝3，

所以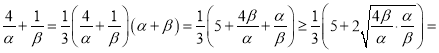3，

当且仅当，即α＝2，β＝1时取等号，

所以．