题目内容
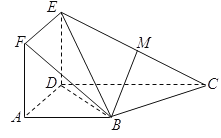
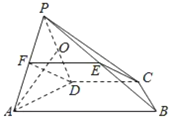
【题目】如图所示,四棱锥![]() 的底面是梯形,且
的底面是梯形,且![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 中点,
中点,![]() .
.
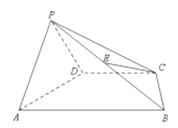
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的高.
的高.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,可得
,可得![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() ,根据
,根据![]() 平面
平面![]() ,得到
,得到![]() ,从而得到
,从而得到![]() .(2)设点
.(2)设点![]() 为
为![]() 的中点,连结
的中点,连结![]() ,证明
,证明![]() 为正三角形,推出
为正三角形,推出![]() ,求出
,求出![]() ,再证明
,再证明![]() ,从而得到
,从而得到![]() 平面
平面![]() ,然后得到三棱锥
,然后得到三棱锥![]() 的高.
的高.
(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,如图所示.
,如图所示.
因为点![]() 是
是![]() 中点,
中点,
所以![]() 且
且![]() .
.
又因为![]() 且
且![]() ,
,
所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
所以![]() .
.
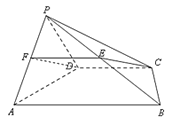
(2)解:设点![]() 为
为![]() 的中点,连结
的中点,连结![]() ,如图所示,
,如图所示,
因为![]() ,
,![]() ,
,
由(1)知,![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 为正三角形,
为正三角形,
所以![]() ,且
,且![]() .
.
因为![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
所以三棱锥![]() 的高为
的高为![]() .
.

练习册系列答案
相关题目
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
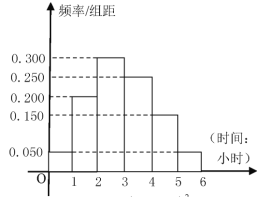
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附:
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |