题目内容
已知正方形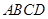 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点.
(1)在正方形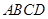 内部随机取一点
内部随机取一点 ,求满足
,求满足 的概率;
的概率;
(2)从 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
(1)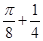 ;(2)详见解析
;(2)详见解析
解析试题分析:(1)首先判断这是一个几何概型,然后找出符合条件的区域与总区域的面积,利用面积之比即可算出相应的古典概型的概率;(2)先确定这八个点连线距离的几种情况,然后就不同的 为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人) 的值进行计算,利用离散型随机变量的计算方法列表并计算相应的数学期望。
的值进行计算,利用离散型随机变量的计算方法列表并计算相应的数学期望。
试题解析:(1)这是一个几何概型.所有点 构成的平面区域是正方形
构成的平面区域是正方形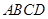 的内部,其面积是
的内部,其面积是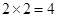 .
.
1分
满足 的点
的点 构成的平面区域是以
构成的平面区域是以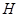 为圆心,
为圆心,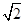 为半径的圆的内部与正方形
为半径的圆的内部与正方形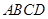 内部的公共部分,它可以看作是由一个以
内部的公共部分,它可以看作是由一个以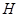 为圆心、
为圆心、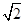 为半径、圆心角为
为半径、圆心角为 的扇形
的扇形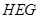 的内部(即四分之一个圆)与两个直角边为1的等腰直角三角形(△
的内部(即四分之一个圆)与两个直角边为1的等腰直角三角形(△ 和△
和△ )内部构成. 2分
)内部构成. 2分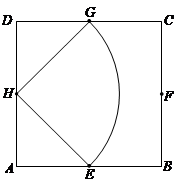
其面积是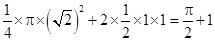 . 3分
. 3分
所以满足 的概率为
的概率为 . 4分
. 4分
(2)从 这八个点中,任意选取两个点,共可构成
这八个点中,任意选取两个点,共可构成 条不同的线段.
条不同的线段.
5分
其中长度为1的线段有8条,长度为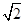 的线段有4条,长度为2的线段有6条,长度为
的线段有4条,长度为2的线段有6条,长度为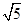 的线段有8条,长度为
的线段有8条,长度为 的线段有2条.
的线段有2条.
所以 所有可能的取值为
所有可能的取值为 . 7分
. 7分
且 ,
,  ,
,  ,
,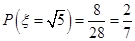 ,
, 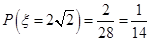 . 9分
. 9分
所以随机变量 的分布列为:
的分布列为:

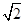
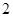
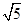






名师点拨组合阅读训练系列答案
名校1号快乐暑假学年总复习系列答案
新暑假生活系列答案
蓝博士暑假生活甘肃少年儿童出版社系列答案

假期生活北京教育出版社系列答案
暑假作业武汉出版社系列答案
暑假学习与生活山东友谊出版社系列答案
成长记暑假总动员云南科技出版社系列答案
课课练检测卷系列答案
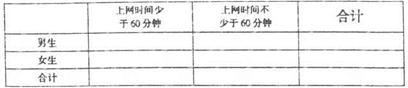
高校
相关人数
抽取人数
A
18

B
36
2
C
54
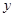
(1)求 ,
,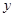 ;
;
(2)若从高校B、C抽取的人中选2人作专题发言,
求这2人都来自高校C的概率.
 的概率分布列及期望.
的概率分布列及期望.



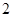 个白球和
个白球和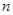 个红球
个红球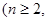 且
且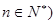 ,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.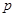 ;
;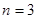 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;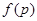 ,当
,当

 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 四个数中任取的一个数,求
四个数中任取的一个数,求 为偶函数的概率;
为偶函数的概率; ,
, 任取的一个数,求方程
任取的一个数,求方程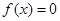 有实根的概率.
有实根的概率.