题目内容
一个口袋中有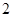 个白球和
个白球和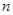 个红球
个红球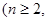 且
且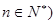 ,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(Ⅰ)试用含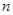 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率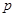 ;
;
(Ⅱ)若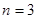 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(Ⅲ)记三次摸球恰有一次中奖的概率为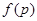 ,当
,当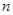 为何值时,
为何值时,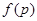 取最大值.
取最大值.
(Ⅰ)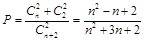 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ)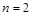 .
.
解析试题分析:(Ⅰ)先求出总事件为 ,两球颜色相同的事件有
,两球颜色相同的事件有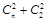 ,然后得到结果;
,然后得到结果;
(Ⅱ)先求出一次模球中奖的概率,又三次是独立重复试验,故可求得三次摸球中恰有一次中奖的概率;
(Ⅲ)先表示出三次摸球中恰有一次中奖的概率,再根据单调性就可求得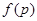 的最大值.
的最大值.
试题解析:(Ⅰ)一次摸球从 个球中任选两个,有
个球中任选两个,有 种选法,其中两球颜色相同有
种选法,其中两球颜色相同有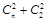 种选法;
种选法;
一次摸球中奖的概率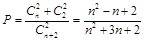 , 4分
, 4分
(Ⅱ)若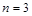 ,则一次摸球中奖的概率是
,则一次摸球中奖的概率是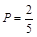 ,三次摸球是独立重复实验,三次摸球中恰有一次中奖的概率是
,三次摸球是独立重复实验,三次摸球中恰有一次中奖的概率是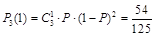 . 8分
. 8分
(Ⅲ)设一次摸球中奖的概率是 ,则三次摸球中恰有一次中奖的概率
,则三次摸球中恰有一次中奖的概率
是
 ,
,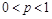 ,
, ,
, 在
在 是增函数,在
是增函数,在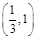 是减函数,
是减函数,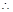 当
当 时,
时, 取最大值 , 10分
取最大值 , 10分
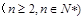 ,
,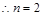 ,故
,故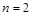 时,三次摸球中恰有一次中奖的概率最大. 12分
时,三次摸球中恰有一次中奖的概率最大. 12分
考点:1.古典概型; 2.独立重复试验.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况,得右表:
| | 偏瘦 | 正常 | 肥胖 |
| 女生(人) | 300 | 865 |  |
| 男生(人) | 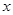 | 885 | 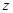 |
(Ⅰ)求
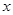 的值;
的值;(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽出多少名?
(Ⅲ)已知
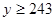 ,
,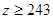 ,求肥胖学生中男生不少于女生的概率.
,求肥胖学生中男生不少于女生的概率. (12分)某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(Ⅰ)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(Ⅱ)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |

根据以往资料统计,大学生购买某品牌平板电脑时计划采用分期付款的期数ζ的分布列为
| ζ | 1 | 2 | 3 |
| P | 0.4 | 0.25 | 0.35 |
(2)若签订协议后,在实际付款中,采用1期付款的没有变化,采用2、3期付款的都至多有一次改付款期数的机会,其中采用2期付款的只能改为3期,概率为
 ;采用3期付款的只能改为2期,概率为
;采用3期付款的只能改为2期,概率为 .数码城销售一台该平板电脑,实际付款期数
.数码城销售一台该平板电脑,实际付款期数 与利润
与利润 (元)的关系为
(元)的关系为 | 1 | 2 | 3 |
| η | 200 | 250 | 300 |
 的分布列及期望E(
的分布列及期望E( ).
).  只,其中有
只,其中有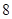 只合格品,
只合格品, 只次品。
只次品。 次,每次取一只灯泡,求
次,每次取一只灯泡,求 的分布列和数学期望.
的分布列和数学期望. 个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得
个,每个选择题给出了四个选项,在给出的四个选项中,只有一项是符合题目要求的. 评分标准规定:对于每个选择题,不选或多选或错选得 分,选对得
分,选对得 分.在这次考试的选择题部分,某考生比较熟悉其中的
分.在这次考试的选择题部分,某考生比较熟悉其中的 个题,该考生做对了这
个题,该考生做对了这 个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题:
个题,有一个题,因全然不理解题意,该考生在给出的四个选项中,随机选了一个;有一个题给出的四个选项,可判断有一个选项不符合题目要求,该考生在剩下的三个选项中,随机选了一个;还有两个题,每个题给出的四个选项,可判断有两个选项不符合题目要求,对于这两个题,该考生都是在剩下的两个选项中,随机选了一个选项.请你根据上述信息,解决下列问题: 分的概率;
分的概率; ,求
,求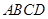 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点. ,求满足
,求满足 的概率;
的概率; 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为 ,求随机变量
,求随机变量 .
.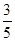 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是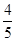 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用 表示张同学答对题的个数,求
表示张同学答对题的个数,求