Question

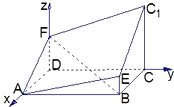
【题目】如图所示的多面体是由底面为的长方体被截面所截面而得到的，其中

（1）求的长；

（2）求点到平面的距离.

Answer 1

【答案】（1）；（2）

【解析】

以为坐标原点，分别以为轴，建立空间直角坐标系，

（1）由为平行四边形，运用向量的模的计算方法，可得的长度；
（2）运用向量坐标运算计算点到平面的距离．

(1)建立如图所示的空间直角坐标系，则D(0，0，0)，B(2，4，0)，A(2，0，0)，C(0，4，0)，E(2，4，1)，C1(0，4，3)．

设F(0，0，z)．

∵AEC1F为平行四边形， ∴由AEC1F为平行四边形，

∴由=得，(-2，0，z)=(-2，0，2)，

∴z=2．∴F(0，0，2)．∴=(-2，-4，2，于是||=2，即BF的长为2；

(2)设为平面AEC1F的法向量，显然不垂直于平面ADF，故可设=(x，y，1)．

，即，∴

又=(0，0，3)，设与的夹角为a， 则cosα==，

∴C到平面AEC1F的距离为d=||cosα=3×=．