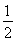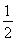Question

已知函数f(x)＝ex，x∈R.

(1)若直线y＝kx＋1与f(x)的反函数的图像相切，求实数k的值；

(2)设x>0，讨论曲线y＝f(x)与曲线y＝mx2(m>0)公共点的个数．

 

Answer 1

（1）k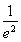＝（2）若0<m<，曲线y＝f(x)与y＝mx2没有公共点；若m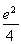＝，曲线y＝f(x)与y＝mx2有一个公共点；若m>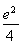，曲线y＝f(x)与y＝mx2有两个公共点

【解析】(1)f(x)的反函数为g(x)＝ln x.

设直线y＝kx＋1与g(x)＝ln x的图像在P(x0，y0)处相切，则有y0＝kx0＋1＝ln x0，k＝g′(x0)＝，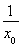

解得x0＝e2，k＝.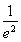

(2)曲线y＝ex与y＝mx2的公共点个数等于曲线y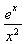＝与直线y＝m的公共点个数．

令φ(x)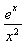＝，则φ′(x)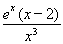＝，∴φ′(2)＝0.

当x∈(0，2)时，φ′(x)<0，φ(x)在(0，2)上单调递减；当x∈(2，＋∞)时，φ′(x)>0，φ(x)在(2，＋∞)上单调递增．

∴φ(x)在(0，＋∞)上的最小值为φ(2)＝.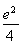

综上所述，当x>0时，大致图像如图所示，

若0<m<，曲线y＝f(x)与y＝mx2没有公共点；

若m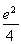＝，曲线y＝f(x)与y＝mx2有一个公共点；

若m>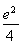，曲线y＝f(x)与y＝mx2有两个公共点