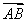题目内容
设函数f(x)=x-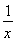 ,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________.
,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________.

【解析】由f(x)=x- ,f(2mx)+2mf(x)<0,可得4mx2<
,f(2mx)+2mf(x)<0,可得4mx2< .若m>0,则x2<
.若m>0,则x2< 不恒成立;若m<0,则x2>
不恒成立;若m<0,则x2> ,当x∈[1,+∞)时,若要使不等式恒成立,则
,当x∈[1,+∞)时,若要使不等式恒成立,则 <1,即m2>
<1,即m2>  ,所以m<-
,所以m<-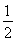 .综上可知m<-
.综上可知m<-

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) | 3 | 4 | 5 | 6 |
销售额y(万元) | 25 | 30 | 40 | 45 |
根据上表可得回归方程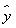 =
=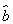 x+
x+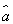 中的
中的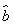 为7.根据此模型,当预报广告费用为10万元时,销售额为________万元.
为7.根据此模型,当预报广告费用为10万元时,销售额为________万元.