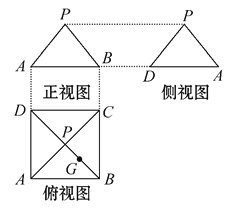
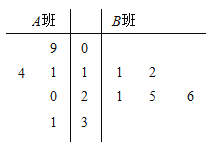
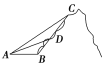
题目内容
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
【答案】(Ⅰ) 当![]() 时,
时, ![]() 的增区间为
的增区间为![]() 和
和![]() .
.
当a>0时,![]() 增区间为
增区间为![]() 和
和![]() ,减区间为
,减区间为![]() 和
和![]()
(Ⅱ)![]() .
.
【解析】(Ⅰ) ![]()
①当![]() 时,
时,![]() 恒成立,
恒成立,
于是![]() 的增区间为
的增区间为![]() 和
和![]() .
.
②当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() .列表得
.列表得
|
|
|
|
|
|
|
| + | 0 | - | - | 0 | + |
| ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
于是![]() 增区间为
增区间为![]() 和
和![]() ,
,
减区间为![]() 和
和![]()
综上可得, 当![]() 时,
时, ![]() 的增区间为
的增区间为![]() 和
和![]() .
.
当![]() 时,
时,![]() 增区间为
增区间为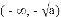 和
和![]() ,减区间为
,减区间为![]() 和
和![]()
(Ⅱ)当![]() 时,对于任意
时,对于任意![]() 时,不等式
时,不等式![]() 恒成立等价于
恒成立等价于![]()
因为![]() ,所以
,所以![]() 在
在![]() 上递增.
上递增.
所以![]()
由(Ⅰ)知
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]()
![]()
故![]() 时,
时,![]() 成立.
成立.
②当![]() ,
, ![]()
当![]() 时,
时,![]() ,
,![]()
![]()
故![]() 时,
时,![]() 成立.
成立.
当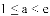 时,
时,![]()
![]() ,得
,得![]() 又
又![]() ,
,
故![]() 时,
时,![]() 成立.
成立.
③当![]() ,即
,即![]() 时,
时,![]()
![]() ,得
,得![]() 与
与![]() 矛盾.
矛盾.
综上所述,存在实数![]() 时,对于任意
时,对于任意![]() 时,不等式
时,不等式![]() 恒成立.
恒成立.
(转化为![]() 恒成立后,用分离参数法求解,比照给分)
恒成立后,用分离参数法求解,比照给分)

【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
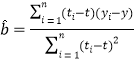 ,
,![]()
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远 (单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳 (单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a-1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A. 2号学生进入30秒跳绳决赛 B. 5号学生进入30秒跳绳决赛
C. 8号学生进入30秒跳绳决赛 D. 9号学生进入30秒跳绳决赛