题目内容
【题目】某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、2万件、1.3万件,为了预测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可以选用二次函数或函数y=abx+c(其中a,b,c为常数),已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好?并说明理由.
【答案】选用y=-0.8×0.5x+1.4作为模拟函数较好.
【解析】试题分析:由题意分别列示求出两种函数模型的待求系数,然后分别取x=4求出相应的函数值,比较大小得答案.
试题解析:
根据题意,该产品的月产量y是月份x的函数,可供选用的函数有两种,其中哪一种函数确定的4月份该产品的产量越接近于1.37万件,哪种函数作为模拟函数就较好,故应先确定这两个函数的具体解析式.
设y1=f(x)=px2+qx+r(p,q,r为常数,
且p≠0),y2=g(x)=abx+c,根据已知有
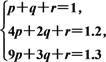 和
和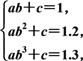
解得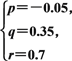 和
和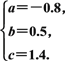
所以f(x)=-0.05x2+0.35x+0.7,g(x)=-0.8×0.5x+1.4.所以f(4)=1.3,g(4)=1.35.
显然g(4)更接近于1.37,故选用y=-0.8×0.5x+1.4作为模拟函数较好.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程。
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式
用最小二乘法求线性回归方程系数公式: ,
, ![]() .
.