题目内容
【题目】已知椭圆![]() 经过点
经过点![]() ,一个焦点为
,一个焦点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)椭圆![]() 的方程是
的方程是![]() ;(2)
;(2)![]() 的取值范围为
的取值范围为![]() .
.
【解析】
试题(1)求椭圆![]() 的方程,已知椭圆
的方程,已知椭圆![]() 经过点
经过点![]() ,一个焦点为
,一个焦点为![]() ,故可用待定系数法,利用焦点为
,故可用待定系数法,利用焦点为![]() 可得
可得![]() ,利用过点
,利用过点![]() ,可得
,可得![]() ,再由
,再由![]() ,即可解出
,即可解出![]() ,从而得椭圆
,从而得椭圆![]() 的方程;(2)求
的方程;(2)求![]() 的取值范围,由弦长公式可求得线段
的取值范围,由弦长公式可求得线段![]() 的长,因此可设
的长,因此可设![]() ,由
,由 得,
得,![]() ,则
,则![]() 是方程的两根,有根与系数关系,得
是方程的两根,有根与系数关系,得![]() ,
,![]() ,由弦长公式求得线段
,由弦长公式求得线段![]() 的长,求
的长,求![]() 的长,需求出
的长,需求出![]() 的坐标,直线
的坐标,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,可得
,可得![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,故先求出线段
,故先求出线段![]() 的中点坐标,写出线段
的中点坐标,写出线段![]() 的垂直平分线方程,令
的垂直平分线方程,令![]() ,既得
,既得![]() 点的坐标,从而得
点的坐标,从而得![]() 的长,这样就得
的长,这样就得![]() 的取值范围.
的取值范围.
试题解析:(1)由题意得 解得
解得![]() ,
,![]() .
.
所以椭圆![]() 的方程是
的方程是![]() . 4分
. 4分
(2)由 得
得![]() .
.
设![]() ,则有
,则有![]() ,
,![]() ,
,
![]() .所以线段
.所以线段![]() 的中点坐标为
的中点坐标为![]() ,
,
所以线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() .
.
于是,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点
轴的交点![]()
![]() ,又点
,又点![]() ,
,
所以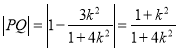 .
.
又![]()
![]() .
.
于是,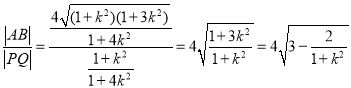 .
.
因为![]() ,所以
,所以![]() .所以
.所以![]() 的取值范围为
的取值范围为![]() . 14分
. 14分

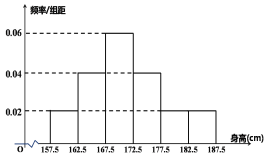
【题目】公历![]() 月
月![]() 日为我国传统清明节,清明节扫墓我们都要献鲜花,某种鲜花的价格会随着需求量的增加而上升.一个批发市场向某地商店供应这种鲜花,具体价格统计如下表所示
日为我国传统清明节,清明节扫墓我们都要献鲜花,某种鲜花的价格会随着需求量的增加而上升.一个批发市场向某地商店供应这种鲜花,具体价格统计如下表所示
日供应量 |
|
|
|
|
|
|
单位 |
|
|
|
|
|
|
(I)根据上表中的数据进行判断,函数模型![]() 与
与![]() 哪一个更适合于体现日供应量
哪一个更适合于体现日供应量![]() 与单价
与单价![]() 之间的关系;(给出判断即可,不必说明理由)
之间的关系;(给出判断即可,不必说明理由)
(II)根据(I)的判断结果以及参考数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(III)该地区有![]() 个商店,其中
个商店,其中![]() 个商店每日对这种鲜花的需求量在
个商店每日对这种鲜花的需求量在![]() 束以下,
束以下,![]() 个商店每日对这种鲜花的需求量在
个商店每日对这种鲜花的需求量在![]() 束以上,则从这
束以上,则从这![]() 个商店个中任取
个商店个中任取![]() 个进行调查,求恰有
个进行调查,求恰有![]() 个商店对这种鲜花的需求量在
个商店对这种鲜花的需求量在![]() 束以上的概率.
束以上的概率.
参考公式及相关数据:对于一组数据![]() ,
,![]() ,...,
,...,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为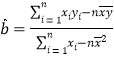 ,
,![]() .
.
|
|
|
|
|
|
|
|