题目内容
14.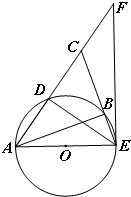 如图,AE是⊙O直径,D是⊙O上一点,连结AD并延长使AD=DC,连结CE交⊙O于点B,连结AB.过点E的直线与AC的延长线交于点F,且∠F=∠CED.
如图,AE是⊙O直径,D是⊙O上一点,连结AD并延长使AD=DC,连结CE交⊙O于点B,连结AB.过点E的直线与AC的延长线交于点F,且∠F=∠CED.(1)求证:EF是⊙O切线;
(2)若CD=CF=2,求BE的长.
分析 (1)证明ED⊥AC.然后证明AE⊥EF.推出EF是⊙O切线.
(2)通过△ADE∽△AEF,求出AE.在Rt△ADE中,求出DE,然后在Rt△ABE中,求解BE.
解答 (本小题满分9分)
(1)证明:∵AE是⊙O直径,∴∠ADE=90°.∴ED⊥AC.
∵AD=DC,∴EA=EC.∴∠AED=∠CED,
∵∠F=∠CED,∴∠AED=∠F.而∠AED+∠EAD=90°,
∴∠F+∠EAD=90°.∴∠AEF=90°.∴AE⊥EF.∴EF是⊙O切线.-----------(4分)
(2)解:∵CD=CF=2,∴AD=CD=CF=2.
∵∠ADE=∠AEF,∠DAE=∠EAF,
∴△ADE∽△AEF.∴AE:AF=AD:AE,即AE:6=2:AE.
∴AE=2$\sqrt{3}$.∴CE=AE=2$\sqrt{3}$.在Rt△ADE中,DE=$\sqrt{{AE}^{2}-{AD}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-{2}^{2}}$=$2\sqrt{2}$.
∵AE是⊙O直径,∴∠ABE=90°.∴$\frac{1}{2}$CE•AB=$\frac{1}{2}$DE•AC,
∴AB=$\frac{2\sqrt{2}×4}{2\sqrt{3}}=\frac{4\sqrt{6}}{3}$.
在Rt△ABE中,BE=$\sqrt{{AE}^{2}-{AB}^{2}}$=$\frac{2\sqrt{3}}{3}$.----------------------(9分)
点评 本题考查直线与圆的位置关系,相似三角形的判断与应用,三角形的解法,考查计算能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
5.已知A,B,P是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率乘积kPA•kPB=$\frac{1}{4}$,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{15}}{3}$ |
2.如图所示的几何体的俯视图是( )
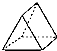

| A. |  | B. |  | C. |  | D. |  |
11.已知Sn是等差数列{an}的前n项和,且a1=-2015,$\frac{{S}_{2014}}{2014}-\frac{{S}_{2013}}{2013}$=1,则S2015的值为( )
| A. | -2014 | B. | 2015 | C. | 2014 | D. | -2015 |
