题目内容
4.计算$\int_0^1{(\frac{1}{2}x}+2)dx$=$\frac{9}{4}$;$\int_{-a}^a{\sqrt{{a^2}-{x^2}}}dx$=$\frac{π{a}^{2}}{2}$.分析 格局定积分的计算以及定积分的几何意义即可求出.
解答 解:$\int_0^1{(\frac{1}{2}x}+2)dx$=($\frac{1}{4}$x2+2x)|${\;}_{0}^{1}$=$\frac{1}{4}$+2=$\frac{9}{4}$;
$\int_{-a}^a{\sqrt{{a^2}-{x^2}}}dx$,表示以原点为圆心以a为半径的圆的面积的一半,
∴$\int_{-a}^a{\sqrt{{a^2}-{x^2}}}dx$=$\frac{1}{2}π$a2,
故答案为:$\frac{9}{4}$,$\frac{π}{2}{a^2}$.
点评 本题考查了定积分的几何意义以及定积分的计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.($\sqrt{x}$+$\frac{1}{\root{3}{x}}$)2n(n∈N*)展开式中只有第6项系数最大,则其常数项为( )
| A. | 120 | B. | 210 | C. | 252 | D. | 45 |
9.复数z=1+2i的实部与虚部分别为( )
| A. | 1,2 | B. | 1,2i | C. | 2,1 | D. | 2i,1 |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的方程是y=$\sqrt{3}$x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程是( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{x^2}{3}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{6}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{16}=1$ |
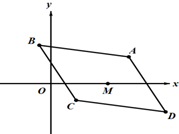 如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)
如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD边所在直线的方程分别是x+4y-7=0,3x+2y-11=0,且对角线AC和BD的交点为M(2,0)