题目内容
设函数f(x)=| 2x-b |
| (x-1)2 |
(1)求函数f(x)的解析式;
(2)若x∈[2,4],求函数的值域;
(3)设a≤
| 1 |
| 2 |
分析:(1)根据函数f(x)图象在x=2处的切线的斜率为2,求导,令f′(2)=2,求得b的值,从而求得函数f(x)的解析式;
(2)求函数f(x)在(2,4)上的极值,再与f(2)、f(4)比较大小,求得函数的值域;(3)由对于任意的x1∈[2,4],总存在x0∈[2,4]使得g(x0)=f(x1)成立,函数g(x)在区间[2,4]上的最大值不小于函数f(x)的最大值,函数g(x)在区间[2,4]上最小值不小于函数f(x)的最小值,转化为求函数g(x)的最值问题.
(2)求函数f(x)在(2,4)上的极值,再与f(2)、f(4)比较大小,求得函数的值域;(3)由对于任意的x1∈[2,4],总存在x0∈[2,4]使得g(x0)=f(x1)成立,函数g(x)在区间[2,4]上的最大值不小于函数f(x)的最大值,函数g(x)在区间[2,4]上最小值不小于函数f(x)的最小值,转化为求函数g(x)的最值问题.
解答:解:(1)f′(x)=
∵f′(2)=2
∴b=4 f(x)=
(2)f′(x)=
=0
即:-2x2+8x-6=0且x≠1
解得:x=3,x=1(舍)
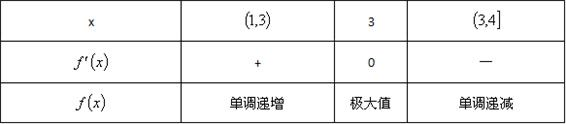
f(x)最大值:f(3)=
f(x)最小值:比较f(2)=0,f(4)=
,所以最小值为f(2)=0;
(3)g(x)=x2-8ax-2a=(x-4a)2-16a2-2a
∵a≤
,x∈[2,4].
∴g(x)min=g(2)=4-18a,
g(x)max=g(4)=16-34a,
∵对于任意的x1∈[2,4],总存在x0∈[2,4]使得g(x0)=f(x1)成立,
∴
,解得
≤a≤
.
∴a的取值范围是
≤a≤
.
| -2x2+2bx-2b+2 |
| (x-1)4 |
∴b=4 f(x)=
| 2x-4 |
| (x-1)2 |
(2)f′(x)=
| -2x2+8x-6 |
| (x-1)4 |
即:-2x2+8x-6=0且x≠1
解得:x=3,x=1(舍)

f(x)最大值:f(3)=
| 1 |
| 2 |
f(x)最小值:比较f(2)=0,f(4)=
| 4 |
| 9 |
(3)g(x)=x2-8ax-2a=(x-4a)2-16a2-2a
∵a≤
| 1 |
| 2 |
∴g(x)min=g(2)=4-18a,
g(x)max=g(4)=16-34a,
∵对于任意的x1∈[2,4],总存在x0∈[2,4]使得g(x0)=f(x1)成立,
∴
|
| 2 |
| 9 |
| 31 |
| 68 |
∴a的取值范围是
| 2 |
| 9 |
| 31 |
| 68 |
点评:考查导数的几何意义,和利用导数研究函数的极值、最值问题,特别是(3)的设问方式,增加了题目的难度,体现了转化的思想方法,属难题.

练习册系列答案
相关题目