题目内容
(考生注意:请在下列三题中任选一题作答,如果多做.则按所做的第一题评阅计分)A.(选修4-4坐标系与参数方程) 已知圆C的圆心为(6,
| π |
| 2 |
| π |
| 2 |
B.(选修4-5 不等式选讲)如果关于x的不等式|x-3|-|x-4|<a的解集不是空集,则实数a的取值范围是
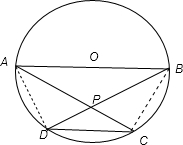
C.(选修4-1 几何证明选讲),AB为圆O的直径,弦AC.BD交于点P,若AB=3,CD=1,则sin∠APD=
分析:A 把方程化为直角坐标方程,由弦长公式求得圆心到直线的距离d,再由点到直线的距离公式求得tana,从而求得a.
B 由于|x-3|-|x-4|的最小值等于-1,不等式|x-3|-|x-4|<a的解集不是空集,则-1<a.
C 由△PAB∽△PDC,可得
=
,由PD⊥AD 可得,cos∠APD=
=
,利用同角三角函数的基本关系求得sin∠APD的值.
B 由于|x-3|-|x-4|的最小值等于-1,不等式|x-3|-|x-4|<a的解集不是空集,则-1<a.
C 由△PAB∽△PDC,可得
| 1 |
| 3 |
| PD |
| PA |
| PD |
| PA |
| 1 |
| 3 |
解答:解:A 由题意得 圆C的圆心为(0,6),圆C的方程为 x2+(y-6)2=25,
直线θ=a(
≤θ<π,ρ∈R) 即 y=tana•x,tana•x-y=0.
设圆心到直线的距离等于d,由弦长公式得 8=2
=2
,∴d=3,
再由点到直线的距离公式得 d=3=
,∴tana=±
.
根据θ范围知,tana<0,∴tana=-
,a=
,故答案为
.
B 由于|x-3|-|x-4|表示数轴上的x到3的距离减去它到4的距离,最小值等于-1,
如果关于x的不等式|x-3|-|x-4|<a的解集不是空集,则-1<a,即 a>-1,故答案为-1.
C 如图所示:由题意得∠APB=∠DPC,∠PDC=∠PAB,∠PCD=∠PBA,
∴△PAB∽△PDC,∴
=
,
=
.∵PD⊥AD(直径对的圆周角等于90°),
∴cos∠APD=
=
,∴sin∠APD=
,故答案为
.
直线θ=a(
| π |
| 2 |
设圆心到直线的距离等于d,由弦长公式得 8=2
| r2-d2 |
| 25-d2 |
再由点到直线的距离公式得 d=3=
| |0-6| | ||
|
| 3 |
根据θ范围知,tana<0,∴tana=-
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
B 由于|x-3|-|x-4|表示数轴上的x到3的距离减去它到4的距离,最小值等于-1,
如果关于x的不等式|x-3|-|x-4|<a的解集不是空集,则-1<a,即 a>-1,故答案为-1.
C 如图所示:由题意得∠APB=∠DPC,∠PDC=∠PAB,∠PCD=∠PBA,
∴△PAB∽△PDC,∴
| CD |
| AB |
| PD |
| PA |
| 1 |
| 3 |
| PD |
| PA |
∴cos∠APD=
| PD |
| PA |
| 1 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |

点评:本题考查绝对值不等式的性质,点到直线的距离公式、弦长公式的应用,体现了数形结合的数学思想.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)