Question

在平面直角坐标系xOy中，已知椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

1

2

，一条准线方程为x=4．
（1）求椭圆E的标准方程；
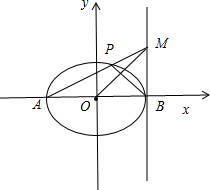
（2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M，设直线OM的斜率为k₁，直线BP的斜率为k₂，求证：k₁k₂为定值．

Answer 1

分析：（1）由题意可得得

c a = 1 2 a2 c =4 a2=b2+c2

，解出即可；
（2）设P（x₀，y₀）（y₀≠0），即可得出直线AP的方程，令x=2，即可得到点M的坐标，利用斜率计算公式即可得出k₁，k₂，再利用点P在椭圆上即可证明．

解答：解：（1）由题意得

c a = 1 2 a2 c =4 a2=b2+c2

，解得

a2=4 b2=3

，∴椭圆E的标准方程为

x2

4

+

y2

3

=1．
（2）设P（x₀，y₀）（y₀≠0），
则直线AP的方程为：y=

y0

x0+2

（x+2）
令x=2得M（2，

4y0

x0+2

）
∴k₁=

2y0

x0+2

，
∵k₂=

y0

x0-2

，
∴k₁k₂=

2 y 2 0

x 2 0 -4

，
∵P（x₀，y₀）在椭圆上，∴

x02

4

+

y02

3

=1
∴k₁k₂═-

3

2

为定值．

点评：熟练掌握椭圆的标准方程及其性质、直线的斜率公式等是解题的关键．