题目内容
20．
如图，已知三棱台ABC-A′B′C′．（1）把它分成一个三棱柱和一个多面体，并用字母表示；
（2）把它分成三个三棱锥，并用字母表示．
分析 根据棱台的几何特征和棱锥的几何特征，先将棱台分成一个三棱锥和四棱锥，再把四棱锥沿对角面切开，可得答案．
解答 解：（1）作B′E交AB′于点E，C′D交AC′于点D，如图所示：
则分成一个三棱柱AED-A′B′C′，和一个多面体C′-DECB．
（2）如下图所示：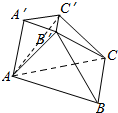
平面AB′C′和平面AB′C能把三棱台分成三部分，分别为三棱锥AA′C′-B′，三棱锥ACC′-B′，三棱锥ABC-B′．
点评 本题考查的知识点是棱台的几何特征，棱锥的几何特征，难度不大，属于基础题．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
11．上饶某中学研究性学习小组为调查市民喜欢观看体育节目是否与性别有关，随机抽取了55名市民，得到数据如下表：
（1）判断是否有99.5%的把握认为喜欢观看体育节目与性别有关？
（2）用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求男市民人数ξ的分布列和期望．
下面的临界值表参考：
| 喜欢 | 不喜欢 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
（2）用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求男市民人数ξ的分布列和期望．
下面的临界值表参考：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5．设经过定点P（a，0）的直线与抛物线y2=6x相交于A，B两点，若$\frac{1}{|PA{|}^{2}}+\frac{1}{|PB{|}^{2}}$为定值，则a=（ ）
| A． | 6 | B． | 3 | C． | $\frac{3}{2}$ | D． | 1 |