题目内容
在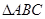 中,角
中,角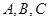 所对的边分别是
所对的边分别是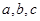 ,已知
,已知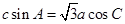 .
.
(Ⅰ)求 ;
;
(Ⅱ)若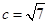 ,且
,且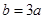 ,求
,求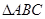 的面积.
的面积.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)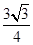 .
.
解析试题分析:本题主要考查解三角形中的正弦定理和余弦定理的应用,以及利用边和夹角的正弦求三角形的面积.第一问由正弦定理把边转化为角,在等式两边消元时,注意消去的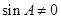 ;第二问,利用余弦定理和第一问的结论先求出
;第二问,利用余弦定理和第一问的结论先求出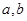 边长,利用
边长,利用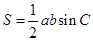 求三角形面积.
求三角形面积.
试题解析:(Ⅰ)由已知及正弦定理,有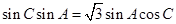 ,因为
,因为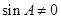 ,解得
,解得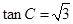 ,
, . 6分
. 6分
(Ⅱ)由余弦定理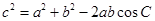 及
及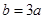 ,解得
,解得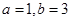 .故
.故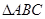 的面积
的面积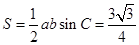 . 12分
. 12分
考点:1.正弦定理;2.余弦定理;3.三角形面积公式.

练习册系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 .
. 的值;
的值; ,求
,求 和
和 的值.
的值. 中,已知
中,已知
 ;
; ,
, ,求
,求 .
. 中,
中, 边上的中线
边上的中线 长为3,且
长为3,且 ,
, .
.
 的值;(Ⅱ)求
的值;(Ⅱ)求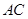 边的长.
边的长. 中,
中, 、
、 、
、 分别是三内角
分别是三内角 、
、 、
、 的对边,已知
的对边,已知 .
. ,判断
,判断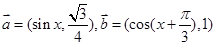 ,函数
,函数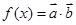 .
.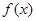 的最值和单调递减区间;
的最值和单调递减区间;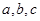 ,
,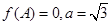 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值. 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知 .
. ;
; ,求△
,求△ 的角
的角 所对的边
所对的边 ,且
,且 .
. 的大小;
的大小; ,求
,求 的最大值并判断这时三角形的形状.
的最大值并判断这时三角形的形状.  =
= .
.