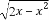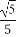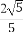题目内容
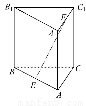
在四棱锥P -ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.
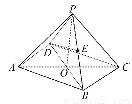
(1)求四棱锥的体积.
(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.
(1)2 (2)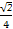
【解析】(1)在四棱锥P-ABCD中,
∵PO⊥平面ABCD,
∴∠PBO是PB与平面ABCD所成的角,
即∠PBO=60°.
在Rt△POB中,
∵BO=AB·sin30°=1,
又PO⊥OB,
∴PO=BO·tan60°=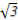 ,
,
∵底面菱形的面积S菱形ABCD=2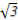 .
.
∴四棱锥P -ABCD的体积
VP -ABCD=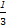 ×2
×2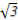 ×
×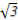 =2.
=2.
(2)取AB的中点F,连接EF,DF,
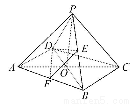
∵E为PB中点,
∴EF∥PA.
∴∠DEF为异面直线DE与PA所成角(或补角).
在Rt△AOB中,
AO=AB·cos30°=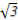 =OP,
=OP,
∴在Rt△POA中,PA=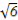 ,
,
∴EF= .
.
∵四边形ABCD为菱形,且∠DAB=60°,
∴△ABD为正三角形.
又∵∠PBO=60°,BO=1,
∴PB=2,∴PB=PD=BD,即△PBD为正三角形,
∴DF=DE=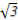 ,
,
∴cos∠DEF=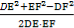
=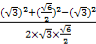 =
=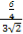 =
=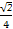 .
.
即异面直线DE与PA所成角的余弦值为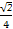 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目