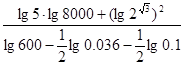题目内容
提高大桥的车辆通行能力可改善整个城市的交通状况.一般情况下,大桥上的车流
速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当车流密度不超过50辆/千米时,车流速度为30千米/小时.研究表明:当50<x≤200时,车流速度v与车流密度x满足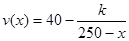 .当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
(Ⅰ)当0<x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上观测点的车辆数,单位:
辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到个位,参考数据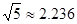 )
)
(1) 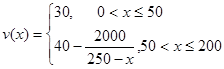 .
.
(2)当车流密度为138 辆/千米时,车流量可以达到最大,最大值约为3056辆/千米时。
解析试题分析:(1) 由题意:当0<x≤50时,v(x)=30;
当50≤x≤200时,由于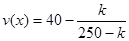 ,
,
再由已知可知,当x=200时,v(0)=0,代入解得k=2000.
故函数v(x)的表达式为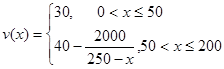 . 6分
. 6分
(2) 依题意并由(1)可得 ,
,
当0≤x≤50时,f(x)=30x,当x=50时取最大值1500. 当50<x≤200时,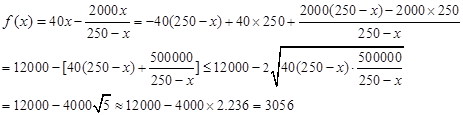
取等号当且仅当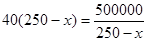 ,即
,即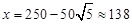 时,f(x)取最大值.
时,f(x)取最大值.
(这里也可利用求导来求最大值)
综上,当车流密度为138 辆/千米时,车流量可以达到最大,最大值约为3056辆/千米时。
考点:本题主要考查分段函数的概念,利用均值定理求函数的最值。
点评:中档题,作为函数的应用问题,确定函数解析式是其一个基本要求,在此基础上,进一步研究函数的图象和性质,确定最值,往往可以应用导数或“均值定理”。应用“均值定理”,要注意“一正,二定,三相等”,缺一不可。

练习册系列答案
相关题目

 ;
; 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围. 与科技成本的投入次数
与科技成本的投入次数 的关系是
的关系是 .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第 万元.
万元.

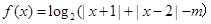 .
.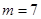 时,求函数
时,求函数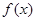 的定义域;
的定义域; 的不等式
的不等式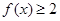 的解集是
的解集是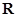 ,求
,求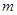 的取值范围.
的取值范围.
 (2)
(2)