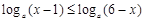题目内容
某商店将进货价10元的商品按每个18元出售时,每天可卖出60个.商店经理到市场做了一番调研后发现,如将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;如将这种商品的售价(在每个18元的基础上)每降低1元,则日销售量就增加10个.为获得每日最大的利润,此商品售价应定为每个多少元?
商品售价应定为每个20元.
解析试题分析:根据提高售价和降低售价后所得利润列出函数关系式,然后分别求出最大值进行比较.设此商品每个售价为x元,每日利润为S元.则当x≥18时有S=[60-5(x-18)](x-10)=-5(x-20)2+500,即当商品提价为20元时,每日利润最大,最大利润为500元;当x<18时有S=[60+10(18-x)](x-10)=-10(x-17)2+490,即当商品降价为17元时,每日利润最大为490元.即综上所得,此商品售价应定为每个20元. 12分
考点:本题主要考查二次函数的图象和性质。
点评:典型题,函数的应用问题,在高考中已渐成固定考查模式,“一大两小”或“两大一小”,主要考查函数模型的构建及问题的解决,有时直接运用二次函数图象和性质可解,有时须应用导数或均值定理等加以解答。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和
和 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点 .
.
 分别对应哪一个函数?
分别对应哪一个函数? ,且
,且 ,指出
,指出 的值,并说明理由;
的值,并说明理由;
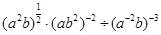 ; (2)计算:
; (2)计算: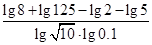 .
. 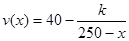 .当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时. 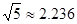 )
)
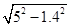 -0.8=4,
-0.8=4, 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域; 元/千克,政府补贴为
元/千克,政府补贴为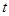 元/千克,根据市场调查,当
元/千克,根据市场调查,当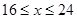 时,这种食品市场日供应量
时,这种食品市场日供应量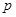 万千克与市场日需量
万千克与市场日需量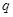 万千克近似地满足关系:
万千克近似地满足关系: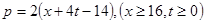 ,
,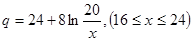 。当
。当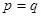 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。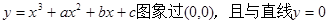 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为 ;
;
 ,当
,当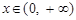 时,有
时,有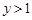 ,解关于x的不等式
,解关于x的不等式