题目内容
已知函数
,则
在
上的零点个数为 ( )
| A．1个 | B．2个 | C．3个 | D．4个 |
B.
解析试题分析：因为f(x)=0,所以f(x)的零点个数即函数
和
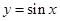在区间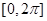
上的交点个数,作出这两个函数的图像可观察到两个函数在区间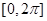上有两个交点，因而f(x)有两个零点。
考点：函数的零点，指数函数的图像，正弦函数的图像。
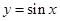点评：根据函数的零点与方程f(x)=0的根的对应关系可知f(x)的零点个数即函数和在区间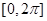上的交点个数,然后借助图像解决即可。
练习册系列答案
相关题目
定义在
上的函数
满足
，当
时，
，当
时，
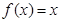，则
| A．335 | B．338 | C．1678 | D．2012 |
f (x)＝
(n∈Z)是偶函数，且y＝f(x)在(0，＋∞)上是减函数，则n＝( ).
| A．1 | B．2 | C．1或2 | D．3 |
函数
的定义域为（ ）
| A．[1，3] | B． | C．（1，3） | D． |
的定义域为开区间
，导函数
在
下图是函数f(x)的图象，它与x轴有4个不同的公共点．给出下列四个区间之中，存在不能用二分法求出的零点，该零点所在的区间是( )
| A．[－2.1，－1] | B．[4.1,5] |
| C．[1.9,2.3] | D．[5,6.1] |
规定
表示
两个数中的最小的数，若函数
的图像关于直线
对称，则
的值是（ ）
A． | B． | C． | D． |
已知
，
，
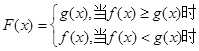，则
的最值是（ ）
A．最大值为3，最小值 | B．最大值为 ，无最小值 |
| C．最大值为3，无最小值 | D．既无最大值，也无最小值 |