题目内容
下图是函数f(x)的图象,它与x轴有4个不同的公共点.给出下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( )
| A.[-2.1,-1] | B.[4.1,5] |
| C.[1.9,2.3] | D.[5,6.1] |
C
解析试题分析:由图象可以看出函数在[-2.1,-1],[1.9,2.3],[4.1,5],[5,6.1]上各有一个零点,而要是在某个区间存在零点,且能用二分法判定,则必有区间的端点值异号。
对比四个选项,C中的零点不能用二分法求,故选C
考点:本题主要考查了二分法求方程的近似解.
点评:解决该试题的关键是掌握好二分法判断零点的原理,明确端点值的函数值是否不是异号即可。正确识图也很关键

练习册系列答案
相关题目
已知函数 为奇函数,则
为奇函数,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知函数 则函数零点个数为 ( )
则函数零点个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,则
,则 在
在 上的零点个数为 ( )
上的零点个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设偶函数 的定义域为R,当
的定义域为R,当
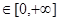 时,
时, 是增函数,则
是增函数,则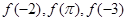 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
下列函数中,值域为(0, )的函数是( )
)的函数是( )
A. | B. | C. | D. |
下列两个函数完全相同的是( )
A. 与 与 | B. 与 与 |
C. 与 与 | D. 与 与 |
已知 是定义在R上不恒为零的偶函数,且对任意
是定义在R上不恒为零的偶函数,且对任意 ,都有
,都有 ,则
,则 的值是( )
的值是( )
| A.0 | B.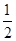 | C.1 | D. |
下列函数中,在其定义域内既是奇函数又是增函数的是( )
A. | B. | C.y=x3 | D. |