题目内容
f (x)= (n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
(n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
| A.1 | B.2 | C.1或2 | D.3 |
C
解析试题分析:结合幂函数的性质可知,若f(x)=x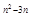 (n∈Z)是偶函数且在(0,+∞)上是减函数,结合n2-3n为整数,可知,n2-3n<0,且n2-3n为偶数,可求.
(n∈Z)是偶函数且在(0,+∞)上是减函数,结合n2-3n为整数,可知,n2-3n<0,且n2-3n为偶数,可求.
:∵f(x)=x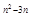 (n∈Z)是偶函数,且n2-3n为整数,∴n2-3n为偶数,又∵y=f(x)在(0,+∞)上是减函数,由幂函数的性质可知,n2-3n<0,即0<n<3
(n∈Z)是偶函数,且n2-3n为整数,∴n2-3n为偶数,又∵y=f(x)在(0,+∞)上是减函数,由幂函数的性质可知,n2-3n<0,即0<n<3
∵n∈Z,则n=1或n=2
当n=1时,n2-3n=-2符合题意;当n=2时,n2-3n=-2,符合题意
故n=1或n=2
故选C
考点:本题主要考查了幂函数的性质的应用.
点评:解答本题的关键是熟练掌握幂函数的性质并能灵活应用.注意幂函数的指数大于零,在第一象限内递增,小于零时,则递减。

练习册系列答案
相关题目
设函数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点 处切线的斜率为 ( )
处切线的斜率为 ( )
| A.2 | B. | C.4 | D. |
已知函数 为奇函数,则
为奇函数,则 的值为( )
的值为( )
A. | B. | C. | D. |
若关于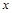 的方程
的方程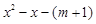 =0在
=0在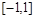 上有解,则
上有解,则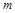 的取值范围是 ( )
的取值范围是 ( )
A.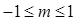 | B.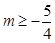 | C. | D.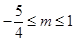 |
对于实数 ,符号
,符号 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,定义函数
,定义函数 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A. | B.方程 有且仅有一个解 有且仅有一个解 |
C.函数 是周期函数 是周期函数 | D.函数 是增函数 是增函数 |
已知函数 则函数零点个数为 ( )
则函数零点个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,则
,则 在
在 上的零点个数为 ( )
上的零点个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知 是定义在R上不恒为零的偶函数,且对任意
是定义在R上不恒为零的偶函数,且对任意 ,都有
,都有 ,则
,则 的值是( )
的值是( )
| A.0 | B.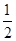 | C.1 | D. |
 与
与 的图象如所示,则函数
的图象如所示,则函数 的图象可能为( )
的图象可能为( )
