题目内容
若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值为________.
9
解析试题分析:由题意,x=1是f′(x)=12x2-2ax-2b的一个零点,所以12-2a-2b=0,即a+b=6(a>0,b>0),因此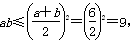 当且仅当a=b=3时等号成立.
当且仅当a=b=3时等号成立.
考点:本题考查了极值的性质及基本不等式的运用
点评:应用基本不等式求最值需注意三个要素:一正、二正、三相等,属基础题

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 满足
满足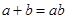 ,
, ,则
,则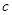 的取值范围是______.
的取值范围是______. 、
、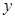 为正整数,且满足
为正整数,且满足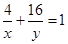 ,则
,则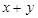 的最小值为_________;
的最小值为_________;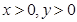 ,且
,且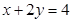 ,则
,则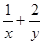 的最小值为
的最小值为 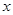 的不等式
的不等式 对一切
对一切 恒成立,则
恒成立,则
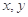 满足
满足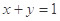 ,且
,且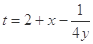 . 则当
. 则当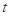 取最大值时
取最大值时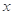 的值为 .
的值为 .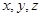 满足
满足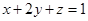 ,则
,则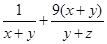 的最小值为 .
的最小值为 .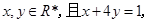 则
则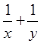 的最小值为
的最小值为 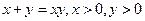 则
则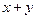 的最小值是 ;
的最小值是 ;