题目内容
若关于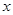
的不等式
对一切
恒成立，则
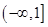
解析试题分析：设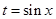
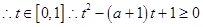恒成立
，
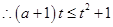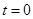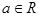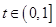时
，
时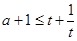
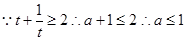
考点：不等式
点评：本题中的不等式恒成立问题转化为求函数最值的问题，结合对勾函数的性质可知函数的最值
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
浙大优学小学年级衔接捷径浙江大学出版社系列答案题目内容
若关于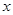的不等式对一切恒成立，则
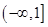
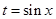
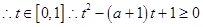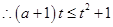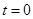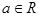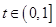解析试题分析：设恒成立，时，时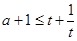
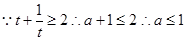
考点：不等式
点评：本题中的不等式恒成立问题转化为求函数最值的问题，结合对勾函数的性质可知函数的最值
浙大优学小学年级衔接捷径浙江大学出版社系列答案
为实常数,
是定义在R上的奇函数,当
时,
, 若
对一切
成立,则
,则
的最小值是 ．
，
，
．则下列不等式：①
； ②
； ③
； ④
.其中成立的是 ．(写出所有正确命题的序号) 
②.y=sin
+
(0<
) ③.y=lgx+4log
10 ④y=5
+45
、
满足
，则
的最小值是 
，则
的最小值为____________
，则
的最小值为