题目内容
若正实数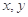 满足
满足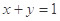 ,且
,且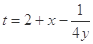 . 则当
. 则当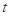 取最大值时
取最大值时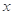 的值为 .
的值为 .
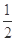
解析试题分析:因为正实数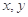 满足
满足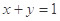 ,所以
,所以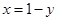 ,
,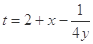 =
=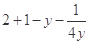 =3-
=3-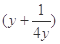 ,而
,而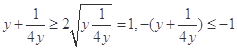 ,故
,故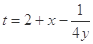
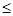 2,其中“=”成立的条件为
2,其中“=”成立的条件为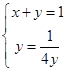 ,解得,
,解得,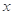 的值为
的值为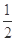 。
。
考点:本题主要考查均值定理的应用。
点评:中档题,应用均值定理,“一正,二定,三相等”缺一不可。解答本题的关键,是通过转化,创造应用均值定理的条件。

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
若正实数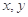 满足
满足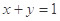 ,且
,且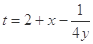 . 则当
. 则当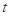 取最大值时
取最大值时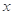 的值为 .
的值为 .
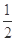
解析试题分析:因为正实数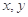 满足
满足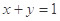 ,所以
,所以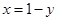 ,
,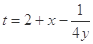 =
=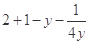 =3-
=3-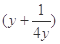 ,而
,而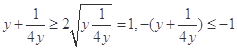 ,故
,故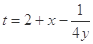
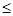 2,其中“=”成立的条件为
2,其中“=”成立的条件为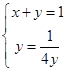 ,解得,
,解得,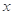 的值为
的值为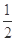 。
。
考点:本题主要考查均值定理的应用。
点评:中档题,应用均值定理,“一正,二定,三相等”缺一不可。解答本题的关键,是通过转化,创造应用均值定理的条件。

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案