题目内容
若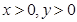 ,且
,且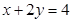 ,则
,则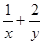 的最小值为
的最小值为

解析试题分析:因为,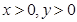 ,且
,且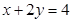 ,
,
所以, ,故答案为
,故答案为 。
。
考点:均值定理的应用。
点评:简单题,应用均值定理,“一正,二定,三相等”,缺一不可。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
题目内容
若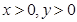 ,且
,且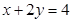 ,则
,则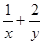 的最小值为
的最小值为

解析试题分析:因为,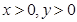 ,且
,且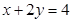 ,
,
所以, ,故答案为
,故答案为 。
。
考点:均值定理的应用。
点评:简单题,应用均值定理,“一正,二定,三相等”,缺一不可。

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案