题目内容
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是| 1 |
| 6 |
| 1 |
| 6 |
分析:根据周角等于360°,得到所有的基本事件对应的图形是360°角的整个平面区域,再根据射线OT落在60°的终边上,得到符合题意的事件对应的图形是所成角为60°的两条射线之间区域.最后用符合题意的图形对应的角度,除以所有的基本事件对应图形的角度,可得OA落在∠xOT内的概率.
解答:解:∵周角等于360°,
∴任作一条射线OA,它的运动轨迹可以绕原点旋转一周,
所以所有的基本事件对应的图形是360°角的整个平面区域.
∵射线OT落在60°的终边上,
∴若OA落在∠xOT内,符合题意的事件对应的图形是所成角为60°的两条射线之间区域,
记事件X=“任作一条射线OA,OA落在∠xOT内”,
可得所求的概率为:P(x)=
=
故答案为:
∴任作一条射线OA,它的运动轨迹可以绕原点旋转一周,
所以所有的基本事件对应的图形是360°角的整个平面区域.
∵射线OT落在60°的终边上,
∴若OA落在∠xOT内,符合题意的事件对应的图形是所成角为60°的两条射线之间区域,
记事件X=“任作一条射线OA,OA落在∠xOT内”,
可得所求的概率为:P(x)=
| 60 |
| 360 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题以作一条射线,求落在指定区域的事件概率为载体,着重考查了用几何图形求概率的知识,属于基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
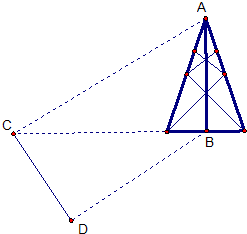 (2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB.
(2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB. (2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )
(2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )