题目内容
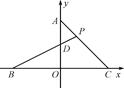
如图，已知A、B、C三点的坐标分别为(0，1)、(－1，0)、(1，0)，P是线段AC上一点，BP交AO于点D，设三角形ADP的面积为S，点P的坐标为(x，y)，求S关于x的函数表达式．
S＝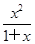
(0<x≤1)
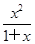(0<x≤1)如图，作PE⊥y轴于E，PF⊥x轴于F，则PE＝x，PF＝y.
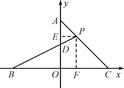
∵OA＝OB＝OC＝1，∴∠ACO＝∠FPC＝45°，
∴PF＝FC＝y，∴OF＝OC－FC＝1－y，
∴x＝1－y，即y＝1－x，∴BF＝2－y＝1＋x.
∵OE∥FP，∴△BOD∽△BFP，∴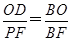
，即
，
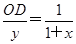∴OD＝
＝
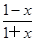，∴AD＝1－OD＝1－＝
，
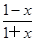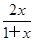S△ADP＝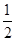
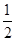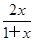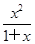AD·PE＝·×x＝，∴S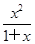＝(0<x≤1)．
∵OA＝OB＝OC＝1，∴∠ACO＝∠FPC＝45°，
∴PF＝FC＝y，∴OF＝OC－FC＝1－y，
∴x＝1－y，即y＝1－x，∴BF＝2－y＝1＋x.
∵OE∥FP，∴△BOD∽△BFP，∴
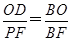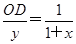，即，∴OD＝
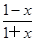＝，∴AD＝1－OD＝1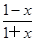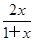－＝，S△ADP＝
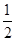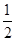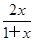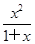AD·PE＝·×x＝，∴S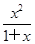＝(0<x≤1)．
练习册系列答案
相关题目
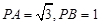，则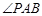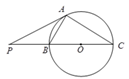
=_________.
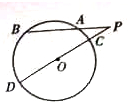
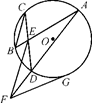
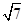的⊙O中，弦AB，CD相交于点P，PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________．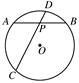
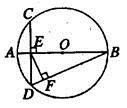
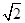，求AF的长．