题目内容
数列{an}的通项公式an=ncos ,其前n项和为Sn,则S2012等于( )
,其前n项和为Sn,则S2012等于( )
 ,其前n项和为Sn,则S2012等于( )
,其前n项和为Sn,则S2012等于( )| A.1006 | B.2012 | C.503 | D.0 |
A
∵当n∈N*时,
a4k+1=(4k+1)cos(2kπ+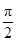 )=0,
)=0,
a4k+2=(4k+2)cos(2kπ+π)=-(4k+2),
a4k+3=(4k+3)cos(2kπ+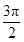 )=0,
)=0,
a4n+4=(4k+4)cos(2kπ+2π)=4k+4,
∴a4k+1+a4k+2+a4k+3+a4k+4=2.
则S2012=(a1+a2+a3+a4)+(a5+a6+a7+a8)+…+(a2009+a2010+a2011+a2012)=2×503=1006.
a4k+1=(4k+1)cos(2kπ+
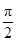 )=0,
)=0,a4k+2=(4k+2)cos(2kπ+π)=-(4k+2),
a4k+3=(4k+3)cos(2kπ+
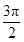 )=0,
)=0,a4n+4=(4k+4)cos(2kπ+2π)=4k+4,
∴a4k+1+a4k+2+a4k+3+a4k+4=2.
则S2012=(a1+a2+a3+a4)+(a5+a6+a7+a8)+…+(a2009+a2010+a2011+a2012)=2×503=1006.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 (2n
(2n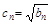 ,
,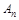 是
是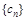 前
前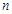 项和,
项和, 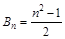 ,当
,当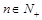 时,试比较
时,试比较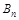 的大小.
的大小. 的首项
的首项 ,
,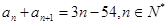
 项和为
项和为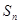 ,求
,求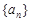 的通项公式
的通项公式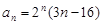 ,则数列
,则数列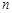 项和
项和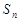 取得最小值时
取得最小值时



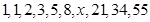 中,
中,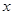 等于( )
等于( )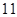



 ,则第2013个数是( )
,则第2013个数是( ) 满足
满足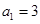 ,
, ,且
,且 ,则
,则