题目内容
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意正整数
,且对任意正整数![]() ,
,![]() 都为
都为![]() 中等于
中等于![]() 的项的个数,则称数列
的项的个数,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)请列举出三个![]() 数列,每个
数列,每个![]() 数列只写出其前5项;
数列只写出其前5项;
(2)若数列![]() 为一个
为一个![]() 数列,证明:
数列,证明:![]() ,都有
,都有![]() ;
;
(3)若数列![]() 为一个
为一个![]() 数列,求集合
数列,求集合![]() 中元素个数的最大值.
中元素个数的最大值.
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)证明见解析;(3)1010.
;(2)证明见解析;(3)1010.
【解析】
(1)根据X数列的定义进行求解即可
(2)根据数列{an}为一个X数列,讨论n是奇数和偶数,分别进行证明即可
(3)根据数列{an}为一个X数列,结合不等式以及集合元素的关系进行求解即可
(1)![]() ;
;![]() ;
;![]() .
.
(2)由题意可知在![]() 中,值为
中,值为![]() 的相邻项至多相邻两项,且至多出现一次.
的相邻项至多相邻两项,且至多出现一次.
①当![]() 为奇数时,
为奇数时,![]() 这
这![]() 组数中,至多有1组数均为
组数中,至多有1组数均为![]() ,
,
所以此时![]() .
.
②当![]() 为偶数时,若
为偶数时,若![]() ,已知
,已知![]() ,所以
,所以![]() 显然成立 ,
显然成立 ,
若![]() ,当
,当![]() ,则
,则![]() 依次为
依次为![]() ;当
;当![]() ,则
,则![]() 依次为
依次为![]()
所以![]() 中必有两项为1,且相邻,
中必有两项为1,且相邻,
所以![]() 这
这![]() 组数中,
组数中,
若![]() ,则
,则![]() 这
这![]() 组数中,每组至多有一项等于
组数中,每组至多有一项等于![]() ,
,
又![]() 中有两项等于
中有两项等于![]() ,所以此时
,所以此时![]() ,
,
若![]() ,则
,则![]() 这
这![]() 组数中,至多有一组全等于
组数中,至多有一组全等于![]() ,
,
又![]() 中至多有一项等于
中至多有一项等于![]() ,此时
,此时![]() ,
,
综上![]() ,
,![]() ,都有
,都有![]() .
.
(3)由(2)可知,![]() ,,
,,
又由题意可知![]() ,所以
,所以![]() ,且
,且![]() ,
,![]() ,
,
所以![]() ,
,
所以集合![]() 中元素个数不大于10101 ,
中元素个数不大于10101 ,
易知当![]() 时,
时,![]() 数列
数列![]() 的前2018项为
的前2018项为![]() .
.
此时![]() 中元素个数等于1010,
中元素个数等于1010,
所以若数列![]() 为一个
为一个![]() 数列,则集合
数列,则集合![]() 中元素个数最大值为1010.
中元素个数最大值为1010.

【题目】已知某校5个学生的数学和物理成绩如下:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学成绩 | 80 | 75 | 70 | 65 | 60 |
物理成绩 | 70 | 66 | 68 | 64 | 62 |
(1)通过大量事实证明发现,一个学生的数学成绩和物理成绩是具有很强的线性相关关系的,在上述表格中,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)利用残差分析回归方程的拟合效果,若残差和在![]() 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
(3)现从5名同学中任选两人参加访谈活动,求1号同学没被选中的概率.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: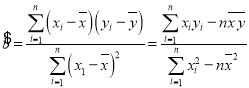 ,
,![]() .
.

