题目内容
从1,2,3,4,5,6中不放回地随机抽取四个数字,记取得的四个数字之和除以4的余数为 ,除以3的余数为
,除以3的余数为
(1)求X=2的概率;
(2)记事件 为事件
为事件 ,事件
,事件 为事件
为事件 ,判断事件
,判断事件 与事件
与事件 是否相互独立,并给出证明.
是否相互独立,并给出证明.
(1)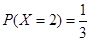 ;(2)事件
;(2)事件 与事件
与事件 不相互独立.
不相互独立.
解析试题分析:(1)求X=2的概率,由题意可知,显然符合古典概型,因此只需列举出所有的基本事件数,与符合条件的基本事件数,根据古典概型概率公式即可求出;(2)判断事件 与事件
与事件 是否相互独立,关键是看
是否相互独立,关键是看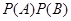 与
与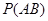 是否相等,利用古典概型概率公式即可求出
是否相等,利用古典概型概率公式即可求出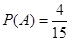 ,
,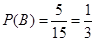 ,及
,及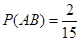 ,可得
,可得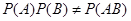 ,从而的结论.
,从而的结论.
试题解析:(1)由题意得基本事件如下(1234)(1235)(1236)(1245)(1246)(1256)(1345)
(1346)(1356)(1456)(2345)(2346)(2356)(2456)(3456)共有15种情况
其中和除以4余2的情况有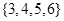 ,
,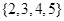 ,
,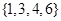 ,
,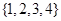 ,
,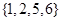 五种情况
五种情况
∴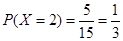 (4分)
(4分)
(2)和为4的倍数的有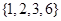 ,
,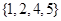 ,
,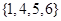 ,
,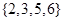 四种情况,
四种情况,
∴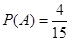 (6分)
(6分)
和为3的倍数的有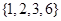 ,
,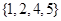 ,
,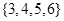 ,
,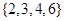 ,
,
五种情况
∴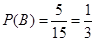 (8分)
(8分)
故即为4的倍数又是3的倍数的有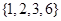 ,
,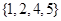 两种情况
两种情况
∴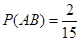 (10分)
(10分)
∵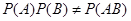 ∴ 事件
∴ 事件 与事件
与事件 不相互独立 (12分)
不相互独立 (12分)
考点:古典概型,独立事件的判断.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
某小组共有A、B、C、D、E五位同学,他们的身高(单位:m)以及体重指标(单位:kg/m2)如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
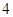 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 .
. ,
, 的值;
的值; 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率; ,求随机变量
,求随机变量 .
.
 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求 ,求随机变量
,求随机变量