题目内容
6．在△ABC中，角A、B、C的对边分别为a、b、c，已知$\frac{3a-b}{cosB}=\frac{c}{cosC}$．（1）求sinC的值；
（2）若c=$\sqrt{3}$，求△ABC的面积S的最大值．
分析 （1）已知等式利用正弦定理化简，整理后根据sinA不为0求出cosC的值，进而确定出sinC的值；
（2）由cosC，c的值，利用余弦定理列出关系式，再利用基本不等式求出ab的最大值，即可确定出S的最大值．
解答 解：（1）已知等式利用正弦定理化简得：$\frac{3sinA-sinB}{cosB}$=$\frac{sinC}{cosC}$，
整理得：3sinAcosC-sinBcosC=sinCcosB，即3sinAcosC=sinBcosC+sinCcosB=sin（B+C）=sinA，
∵sinA≠0，∴cosC=$\frac{1}{3}$，
则sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{2\sqrt{2}}{3}$；
（2）∵c=$\sqrt{3}$，cosC=$\frac{1}{3}$，
∴由余弦定理得：c2=a2+b2-2abcosC，即3=a2+b2-$\frac{2}{3}$ab≥2ab-$\frac{2}{3}$ab=$\frac{4}{3}$ab，
∴ab≤$\frac{9}{4}$，即S$\frac{1}{2}$absinC=$\frac{\sqrt{2}}{3}$ab≤$\frac{3\sqrt{2}}{4}$，
则S的最大值为$\frac{3\sqrt{2}}{4}$．
点评 此题考查了正弦、余弦定理，以及三角形的面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
16．偶函数f（x）=sin（ωx+φ）+cos（ωx+φ）（ω为正整数，|φ|＜$\frac{π}{2}$），且f（x）在（$\frac{π}{6}$，$\frac{π}{3}$）上递减，则f（x）的周期不可能是（ ）
| A． | 2π | B． | π | C． | $\frac{2π}{3}$ | D． | $\frac{π}{2}$ |
1．将函数y=sin2x的图象向右平移$\frac{π}{4}$个单位，再向上平移1个单位，所得函数图象对应的解析式为（ ）
| A． | y=sin（2x-$\frac{π}{4}$）+1 | B． | y=2cos2x | C． | y=1-cos2x | D． | y=-cos2x |
15．
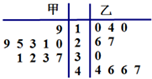从甲、乙两种玉米中各抽测了10株玉米苗的高度（单位：cm），其茎叶图如图所示，根据茎叶图，下列描述正确的是（ ）
从甲、乙两种玉米中各抽测了10株玉米苗的高度（单位：cm），其茎叶图如图所示，根据茎叶图，下列描述正确的是（ ）| A． | 甲种玉米苗的平均高度大于乙种玉米苗的高度，且甲种玉米苗比乙种玉米苗长得整齐 | |
| B． | 甲种玉米苗的平均高度大于乙种玉米苗的高度，但乙种玉米苗比甲种玉米苗长得整齐 | |
| C． | 乙种玉米苗的平均高度大于甲种玉米苗的高度，且乙种玉米苗比甲种玉米苗长得整齐 | |
| D． | 乙种玉米苗的平均高度大于甲种玉米苗的高度，但甲种玉米苗比乙种玉米苗长得整齐 |