题目内容
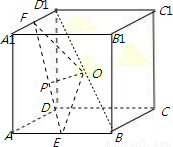
棱长为1的正方体ABCD-A1B1C1D1的八个顶点都在球O的表面上,E、F分别是棱AB、A1D1的中点,则经过E、F的平面截球O所得的截面的面积的最小值是( )A.
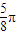
B.
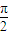
C.
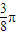
D.
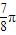
【答案】分析:先求球的半径,再求EF,球心到截面圆的距离,OP,然后求出截面圆的半径,就是图中QP即可.
解答:解:因为正方体内接于球,所以2R=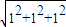 =
=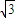 ,R=
,R=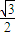 ,
,
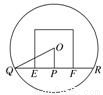
过球心O和点E、F的大圆的截面图如图所示,
则直线被球截得的线段为QR,过点O作OP⊥QR,于点P,EF=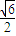 ,OF=
,OF=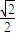
OP=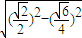 =
=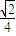 ,所以,在△QPO中,QP=
,所以,在△QPO中,QP=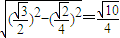 .
.
所以所求经过E、F的平面截球O所得的截面的面积的最小值是: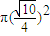 =
=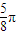 .
.
故选A
点评:本题考查组合体的结构特征,球的内接多面体,截面圆的面积,考查空间想象能力,计算能力,是中档题.
解答:解:因为正方体内接于球,所以2R=
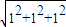 =
=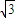 ,R=
,R=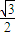 ,
,过球心O和点E、F的大圆的截面图如图所示,
则直线被球截得的线段为QR,过点O作OP⊥QR,于点P,EF=
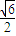 ,OF=
,OF=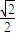
OP=
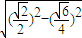 =
=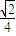 ,所以,在△QPO中,QP=
,所以,在△QPO中,QP=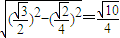 .
.所以所求经过E、F的平面截球O所得的截面的面积的最小值是:
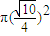 =
=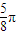 .
.

故选A
点评:本题考查组合体的结构特征,球的内接多面体,截面圆的面积,考查空间想象能力,计算能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
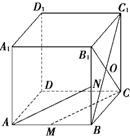 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心. 已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )
已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )