题目内容
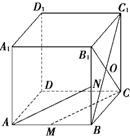 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心.(1)过O作一直线与AN交于P,与CM交于Q(只写作法,不必证明);
(2)求PQ的长.
分析:(1)连接ON,令AD与ON确定的平面为α,O、C、M三点确定的平面为β,由三个平面α,β和ABCD两两相交,故OQ是α与β的交线,连接OQ与AN交于P,与CM交于Q,则直线OPQ即为所求作的直线.
(2)由已知易得△APQ∽△OPN,且相似比为2,由此我们可以求出AP的值,再根据AQ=1,即可求出PQ的值.
(2)由已知易得△APQ∽△OPN,且相似比为2,由此我们可以求出AP的值,再根据AQ=1,即可求出PQ的值.
解答: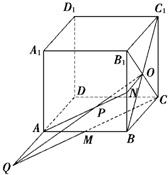 解:(1)连接ON,由ON∥AD知,AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如图所示).
解:(1)连接ON,由ON∥AD知,AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如图所示).
∵三个平面α,β和ABCD两两相交,
有三条交线OP、CM、DA,其中交线DA与交线CM不平行且共面.
∴DA与CM必相交,记交点为Q,∴OQ是α与β的交线.
连接OQ与AN交于P,与CM交于Q,
故直线OPQ即为所求作的直线.
(2)在Rt△APQ中,易知AQ=1,又易知△APQ∽△OPN,
∴
=
=2,AN=
,∴AP=
,
∴PQ=
=
.
 解:(1)连接ON,由ON∥AD知,AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如图所示).
解:(1)连接ON,由ON∥AD知,AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如图所示).∵三个平面α,β和ABCD两两相交,
有三条交线OP、CM、DA,其中交线DA与交线CM不平行且共面.
∴DA与CM必相交,记交点为Q,∴OQ是α与β的交线.
连接OQ与AN交于P,与CM交于Q,
故直线OPQ即为所求作的直线.
(2)在Rt△APQ中,易知AQ=1,又易知△APQ∽△OPN,
∴
| AP |
| PN |
| AQ |
| NO |
| ||
| 2 |
| ||
| 3 |
∴PQ=
| AQ2+AP2 |
| ||
| 3 |
点评:本题考查的知识点是棱柱的结构特征及相似三角形的性质,其中利用公理3确定Q的位置是解答问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
