题目内容
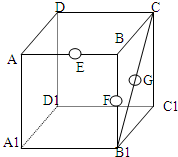 已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )
已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )分析:根据正方体的几何特征,我们选取过E,B1,G三点的平面去截正方体,根据棱锥的体积公式,易求出切下的小三棱锥的体积,进而求出剩下的即容器可装水的容积,进而得到答案.
解答:解:以E,B1,G三点组成的平面去截正方体
截去一个三棱锥
其底面为△EBB1,面积S=
a×1×
=
高为h=1
截去一个三棱锥体积为V=
S•h=
•
•1=
当E,B1,G三点在同一水平面时,F点在水平面之上
E,F,G三点都不漏水
其可装水最大容积1-
=
故选D
截去一个三棱锥
其底面为△EBB1,面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
高为h=1
截去一个三棱锥体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
当E,B1,G三点在同一水平面时,F点在水平面之上
E,F,G三点都不漏水
其可装水最大容积1-
| 1 |
| 12 |
| 11 |
| 12 |
故选D
点评:本题考查的知识点是棱锥的体积,其中根据正方体的几何特征确定出选取过E,B1,G三点的平面去截正方体时,该容器可装水的容积最大是解答本题的关键,本题易将该容器可装水的容积最大时的情况错理解过水面过EFG三点,而错解为B

练习册系列答案
相关题目
 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1. 已知棱长为1的正方体ABCD-A1B1C1D1,O为底ABCD对角线的交点.
已知棱长为1的正方体ABCD-A1B1C1D1,O为底ABCD对角线的交点.