题目内容
已知函数 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求函数 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数 的单调区间.
的单调区间.
(Ⅰ) (Ⅱ)在
(Ⅱ)在 单调减小,在
单调减小,在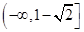 ,
, 单调增加。
单调增加。
解析

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
题目内容
已知函数 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求函数 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数 的单调区间.
的单调区间.
(Ⅰ) (Ⅱ)在
(Ⅱ)在 单调减小,在
单调减小,在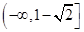 ,
, 单调增加。
单调增加。
解析

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案