题目内容
已知直线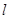 的方程为
的方程为 ,圆
,圆 的方程为
的方程为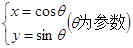 .
.
(1) 把直线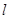 和圆
和圆 的方程化为普通方程;
的方程化为普通方程;
(2) 求圆 上的点到直线
上的点到直线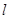 距离的最大值.
距离的最大值.
(1)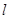 :
: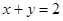 ,
,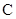 :
: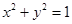 ;(2)
;(2)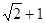 .
.
解析试题分析:(1)以极点为原点,极轴为 轴正半轴建立直角坐标系,利用和角的正弦函数,即可求得该直线的直角坐标方程;利用三角函数的同角关系式中的平方关系,消去圆
轴正半轴建立直角坐标系,利用和角的正弦函数,即可求得该直线的直角坐标方程;利用三角函数的同角关系式中的平方关系,消去圆 的参数方程中的参数,即可得圆
的参数方程中的参数,即可得圆 的普通方程为;(2)求出圆心
的普通方程为;(2)求出圆心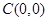 到直线
到直线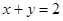 的距离,即可得到圆
的距离,即可得到圆 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
(1)直线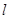 的方程为
的方程为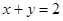 .
.
圆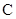 的方程为
的方程为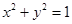 .
.
(2) 易求得圆心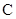 到直线
到直线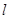 的距离为
的距离为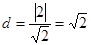 ,
,
所以距离的最大值为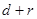 =
=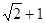 .
.
考点:1、直线与极坐标方程;2、圆的参数方程;3、点到直线的距离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
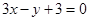 上,若⊿ABC的面积为10,求C点的坐标.
上,若⊿ABC的面积为10,求C点的坐标.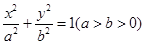 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率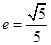 , 直线
, 直线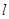 交椭圆于M,N两点.
交椭圆于M,N两点.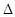 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线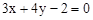 ;
;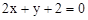 ,它的中心为M
,它的中心为M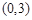 ,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.
,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.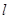 经过点
经过点 ,且斜率为
,且斜率为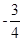 .
.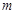 与
与 :
: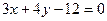 和
和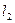 :
: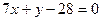 ,则直线
,则直线 夹角为________
夹角为________