题目内容
已知平行四边形ABCD的两条邻边AB、AD所在的直线方程为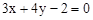 ;
;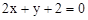 ,它的中心为M
,它的中心为M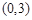 ,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.
,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.
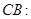
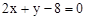 ;
;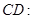
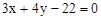 ;平行四边形的面积为40.
;平行四边形的面积为40.
解析试题分析:根据平行四边形的性质可知,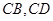 分别与
分别与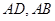 关于点
关于点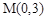 对称,根据对称关系,利用相关点代入法即可求得直线
对称,根据对称关系,利用相关点代入法即可求得直线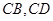 的方程.根据直线的交点,解得
的方程.根据直线的交点,解得 、
、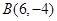 ,所以
,所以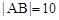 ,而
,而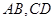 的距离为
的距离为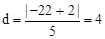 ,故平行四边形的面积为40.
,故平行四边形的面积为40.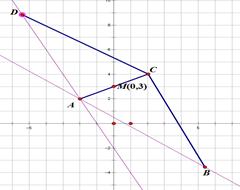
另两边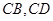 分别与两边
分别与两边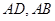 关于点
关于点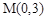 对称,设其上任一点为
对称,设其上任一点为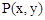 ,则点
,则点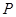 关于M的对称点为
关于M的对称点为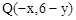 ,由点Q在直线
,由点Q在直线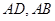 上可得
上可得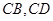 方程分别为:
方程分别为: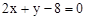 、
、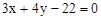 ;联立方程组可得
;联立方程组可得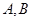 两点坐标分别为
两点坐标分别为 、
、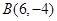 ,所以
,所以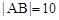 ,而
,而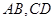 的距离为
的距离为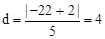 ,故平行四边形的面积为40.
,故平行四边形的面积为40.
考点:直线关于点的对称问题,直线的交点,平行四边形的性质,面积.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
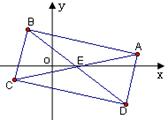
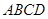 的两条对角线的交点为
的两条对角线的交点为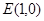 ,且
,且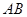 与
与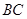 所在的直线方程分别为
所在的直线方程分别为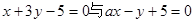 .
.
 所在的直线方程;
所在的直线方程; 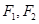 分别为椭圆
分别为椭圆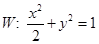 的左、右焦点,斜率为
的左、右焦点,斜率为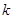 的直线
的直线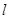 经过右焦点
经过右焦点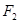 ,且与椭圆W相交于
,且与椭圆W相交于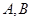 两点.
两点. 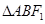 的周长;
的周长; 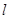 的方程为
的方程为 ,圆
,圆 的方程为
的方程为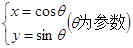 .
.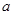 为何值时,直线
为何值时,直线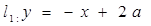 与直线
与直线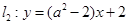 平行?
平行?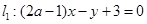 与直线
与直线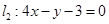 垂直?
垂直?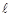 的方程为
的方程为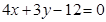 ,求满足下列条件的直线
,求满足下列条件的直线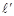 的方程:
的方程: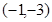 ;(2)
;(2)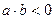 时,如果直线
时,如果直线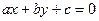 的倾斜角
的倾斜角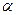 满足关系式
满足关系式 ,则此直线方程的斜率为 ;
,则此直线方程的斜率为 ;