题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)当![]() 时,
时,![]() 单调增区间为
单调增区间为![]() ,无减区间
,无减区间
当![]() 时,
时,![]() 单调增区间为
单调增区间为![]() ,单调减区间为
,单调减区间为![]()
(2)见详解
【解析】
(1) 对函数![]() 求导,
求导,![]() ,讨论
,讨论![]() 与
与![]() 时导函数的正负,来确定函数
时导函数的正负,来确定函数![]() 单调区间。
单调区间。
(2) 将![]() 代入方程,两式相减得
代入方程,两式相减得![]() ,构造
,构造![]()
证明![]() 在定义域内恒成立即可。
在定义域内恒成立即可。
(1)![]()
![]()
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 内单调递增,所以函数
内单调递增,所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
当![]() ,由
,由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调减区间为
,单调减区间为![]() 。
。
(2)因为![]() 是方程
是方程![]() 的两个不相等的实数根,故由(1)得
的两个不相等的实数根,故由(1)得![]() ,
,
不妨设![]() ,则
,则![]() 和
和 ![]()
两式相减可得![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
要证![]() ,只需证
,只需证![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故只需证明![]()
即证明![]() ,设
,设![]() ,即证明
,即证明![]()
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 为增函数,
为增函数,
所以![]() ,即
,即![]() 。
。

【题目】某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位女教师的概率.
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】昆明市某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300),该社团将该校区在2018年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如图4,把该直方图所得频率估计为概率.
空气质量指数 |
|
|
|
|
|
|
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4度中度污染 | 5度重度污染 | 6级严重污染 |
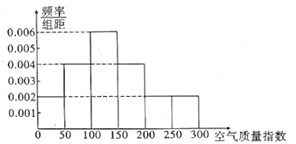
(1)请估算2019年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(2)用分层抽样的方法共抽取10天,则空气质量指数在![]() ,
,![]() ,
,![]() 的天数中各应抽取几天?
的天数中各应抽取几天?
(3)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元若在(2)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用
的天数中任意抽取两天,求这两天的净化空气总费用![]() 的分布列
的分布列