题目内容
【题目】设定义在[﹣2,2]上的奇函数f(x)=x5+x3+b
(1)求b值;
(2)若f(x)在[0,2]上单调递增,且f(m)+f(m﹣1)>0,求实数m的取值范围.
【答案】
(1)解:定义在[﹣2,2]上的奇函数f(x)=x5+x3+b,由于满足f(0)=0,
可得b=0
(2)解:若f(x)在[0,2]上单调递增,且 f(m)+f(m﹣1)>0,
可得f(m)>﹣f(m﹣1)=f(1﹣m),故有 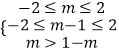 ,
,
解得 ![]() <m≤2,故实数m的范围为(
<m≤2,故实数m的范围为( ![]() ,2]
,2]
【解析】(1)根据奇函数的性质可得f(0)=0,从而求得b的值.(2)由条件可得f(m)>﹣f(m﹣1)=f(1﹣m),再由 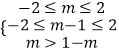 ,求得m的范围.
,求得m的范围.
【考点精析】通过灵活运用函数单调性的性质和函数奇偶性的性质,掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目