题目内容
4．解不等式（x-1）3（x+2）（2x-1）2（x-4）≥0．分析 利用穿根法即可得到结论．
解答 解：对应方程（x-1）3（x+2）（2x-1）2（x-4）=0的根为1，-2，$\frac{1}{2}$，4，
则由穿根法得不等式的解为
-2≤x≤1或x=$\frac{1}{2}$或x≥4，
故不等式的解集为{x|-2≤x≤1或x=$\frac{1}{2}$或x≥4}．
点评 本题主要考查高次不等式的求解，利用穿根法是解决高次不等式的常用方法，注意奇穿偶不穿．
练习册系列答案
相关题目
14．已知函数f（x）=x-2，g（x）=x3+tanx，那么（ ）
| A． | f（x）•g（x）是奇函数 | B． | f（x）•g（x）是偶函数 | C． | f（x）+g（x）是奇函数 | D． | f（x）+g（x）是偶函数 |
矩形ABCD中，AB=6，BC=8，先把它对折，折痕为EF展开后再折成如图所示，使点A落在EF上的点A′处，求第二次折痕BG的长．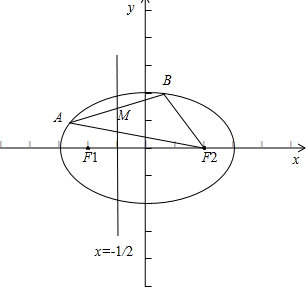
如图，F1，F2是椭圆C：$\frac{{x}^{2}}{2}$+y2=1的左、右焦点，A，B是椭圆C上的两个动点，且线段AB的中点M在直线l：x=-$\frac{1}{2}$上．