题目内容
求函数f(x)=log2x+2x-7的零点个数，并写出它的一个大致区间。
解：设
，可将
的图象作出，如下图所示，
由图可知y1与y2只有一个交点，则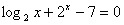
有一个根，
∴函数f(x)有一个零点，
又
，
∴
，
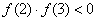∴零点的一个大致区间为(2，3)。
，可将的图象作出，如下图所示， 由图可知y1与y2只有一个交点，则
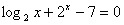有一个根， ∴函数f(x)有一个零点，
又
，∴
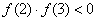，∴零点的一个大致区间为(2，3)。
练习册系列答案
世纪百通期末金卷系列答案
相关题目
(x2－2ax＋3)．
(m∈R)
[8－f(x)]在[1，＋∞)上是单调减函数，求实数m的取值范围；
上的最大值．
)＋4sin(x＋
)－a，把函数y＝g(x)的图象按向量
(－
，1)平移后得到y＝f(x)的图象．
[f(x)＋8＋a]的值域；
，
]时f(x)＝0恒有解，求实数a的取值范围．
的奇函数，a为常数，
)x＋m恒成立，求实数m的取值范围．
）2+7lo
+3≤0的解集为M，求当x∈M时，函数f（x）=（lo
）（lo
）的最大值和最小值．