题目内容
已知函数![]() (m∈R)
(m∈R)
(1)若y=lo![]() [8-f(x)]在[1,+∞)上是单调减函数,求实数m的取值范围;
[8-f(x)]在[1,+∞)上是单调减函数,求实数m的取值范围;
(2)设g(x)=f(x)+lnx,当m≥-2时,求g(x)在![]() 上的最大值.
上的最大值.
答案:
解析:
解析:
解:(1)因为函数![]() 在
在![]() 上是单调减函数,则根据复合函数的单调性可得
上是单调减函数,则根据复合函数的单调性可得![]() 在
在![]() 上是单调减函数,其导数在
上是单调减函数,其导数在![]() 上恒小于等于0,且满足
上恒小于等于0,且满足![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 恒成立,即
恒成立,即![]() 在
在![]() 上恒成立,解得
上恒成立,解得![]()
要使![]() 在
在![]() 上恒成立,只需要
上恒成立,只需要![]() ,又
,又![]() 在
在![]() 上单调减函数,
上单调减函数,![]() ,解得
,解得![]() ,
,![]()
(2)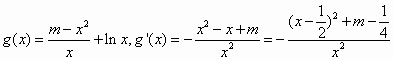
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]()
当![]() 时,由
时,由![]() 得
得![]() ,
,
显然![]() ,又
,又![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;(注意画草图,利用数形结合)
单调递增;(注意画草图,利用数形结合)
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
![]() 综上所述,(1)当
综上所述,(1)当![]() 时,
时,![]() ;
;
(2)当![]() 时,
时,![]()

练习册系列答案
相关题目